Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh góc vuông – góc nhọn. Phân tích và giải Giải bài 2 (4.21) trang 70 vở thực hành Toán 7 – Bài 15. Các trường hợp bằng nhau của tam giác vuôn. Bài 2 (4.21). Cho các điểm A, B,C,D,E như hình bên. Chứng minh rằng \(\Delta ABE = \Delta DCE\)….
Đề bài/câu hỏi:
Bài 2 (4.21). Cho các điểm A, B,C,D,E như hình bên. Chứng minh rằng \(\Delta ABE = \Delta DCE\).
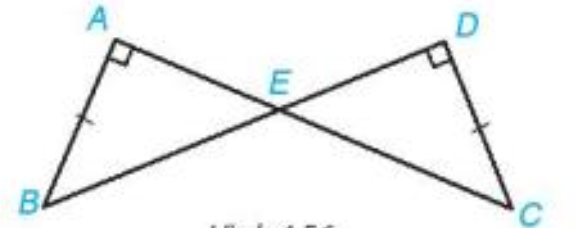
Hướng dẫn:
Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh góc vuông – góc nhọn.
Lời giải:
Theo hình vẽ ta có \(\widehat {AEB} = \widehat {DEC}\)(hai góc đối đỉnh)
Ta thấy hai tam giác ABE và DCE lần lượt vuông tại các đỉnh A, D ta có:
AB = DC (theo giả thiết)
\(\widehat {ABE} = {90^o} – \widehat {AEB} = {90^o} – \widehat {DEC} = \widehat {DCE}\)
Vậy \(\Delta ABE = \Delta DCE\)(cạnh góc vuông – góc nhọn).