Đáp án Luyện tập 1 Bài 9. Hai đường thẳng song song và dấu hiệu nhận biết (trang 46, 47) – SGK Toán 7 Kết nối tri thức. Gợi ý: Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau.
Câu hỏi/Đề bài:
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
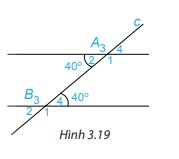
Hướng dẫn:
Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau
Đường thẳng c cắt 2 đường thẳng, tạo thành 1 cặp góc so le trong bằng nhau.
Lời giải:
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ – 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{A_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)