Giải Hoạt động 2 Bài 35. Sự đồng quy của ba đường trung trực – ba đường cao trong một tam giác (trang 77) – SGK Toán 7 Kết nối tri thức. Hướng dẫn: Gọi M là trung điểm BC, N là trung điểm AC.
Câu hỏi/Đề bài:
Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1 bằng cách trả lời các câu hỏi sau:
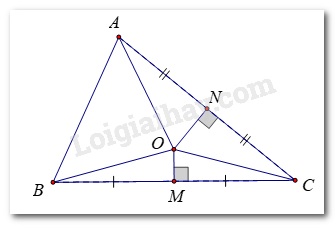
Cho O là giao điểm các đường trung trực của hai cạnh BC và CA (H.9.38)
a) Tại sao OB = OC, OC = OA.
b) Điểm O có nằm trên đường trung trực của AB không?
Hướng dẫn:
Gọi M là trung điểm BC, N là trung điểm AC
a) Chứng minh \(\Delta OBM = \Delta OCM\)(c – g – c), \(\Delta OAN = \Delta OCN\)(c – g – c)
b) Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đấy.
Lời giải:
a)
Gọi M là trung điểm của BC, N là trung điểm AC.
Xét \(\Delta OBM\) và \(\Delta OCM\) có:
BM = CM (gt)
\(\widehat {OMB} = \widehat {OMC} = {90^0}\)
OM chung
\( \Rightarrow \Delta OBM = \Delta OCM\left( {c – g – c} \right)\)
\( \Rightarrow OB = OC\)(cạnh tương ứng)
Chứng minh tương tự: \(\Delta OAN = \Delta OCN\) (c – g – c) \( \Rightarrow OA = OC\) (cạnh tương ứng)
b) Ta có: \(\left\{ \begin{array}{l}OA = OC\\OB = OC\end{array} \right.\left( {cmt} \right) \Rightarrow OA = OB\)
\( \Rightarrow O\) cách đều hai đầu mút của đoạn thẳng AB
\( \Rightarrow O\) nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng)