BD = 2 DC, BC là đường trung tuyến từ đó chứng minh được D là trọng tâm tam giác ABE -AD là phân giác. Lời giải Giải bài 9.39 trang 84 SGK Toán 7 tập 2 – Kết nối tri thức – Bài tập cuối Chương 9. Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC….
Đề bài/câu hỏi:
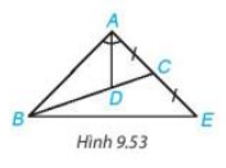
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A
Gợi ý D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Hướng dẫn:
-BD = 2 DC, BC là đường trung tuyến từ đó chứng minh được D là trọng tâm tam giác ABE
-AD là phân giác góc ABE
Lời giải:
C là trung điểm của AE
\( \Rightarrow \) BC là trung tuyến của tam giác ABE (1)
D thuộc BC, \(BD = 2DC \Rightarrow BD = 2\left( {BC – BD} \right) \Rightarrow 3BD = 2BC \Rightarrow BD = \dfrac{2}{3}BC\)(2)
Từ (1) và (2) suy ra: D là trọng tâm của tam giác ABE
\( \Rightarrow \) AD là đường trung tuyến ứng với BE
Mà AD là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \) Tam giác ABE cân tại A.