\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\) -Chứng minh . -\(\widehat {ABD} = {180^0} – 2\widehat {ADB}\). Hướng dẫn cách giải/trả lời Giải bài 9.37 trang 84 SGK Toán 7 tập 2 – Kết nối tri thức – Bài tập cuối Chương 9. Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC,…
Đề bài/câu hỏi:
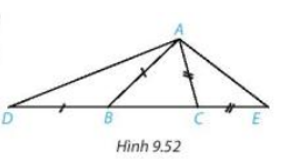
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
Hướng dẫn:
a) \(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)
-Chứng minh .
-\(\widehat {ABD} = {180^0} – 2\widehat {ADB}\),\(\widehat {ACE} = {180^0} – 2\widehat {AEC}\)
b)Sử dụng kết quả câu a)
Lời giải:
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} – \widehat {ABD} \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} – 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} – 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} – 2\widehat {ADB} > {{180}^0} – 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).