\(At\parallel BC\) \(\widehat {ABC} = \widehat {BAt}\)(Hai góc so le trong) \(\widehat {ACB} = \widehat {MAt}\. Lời giải Giải bài 9.34 trang 83 SGK Toán 7 tập 2 – Kết nối tri thức – Luyện tập chung trang 82. Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của AC….
Đề bài/câu hỏi:
Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.
Hướng dẫn:
\(At\parallel BC\)
\(\widehat {ABC} = \widehat {BAt}\)(Hai góc so le trong)
\(\widehat {ACB} = \widehat {MAt}\)(Hai góc đồng vị)
Lời giải:
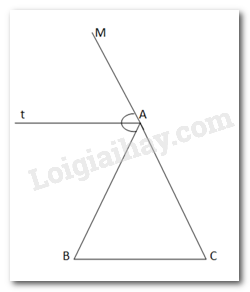
Gọi AM là tia đối của AC. At là đường phân giác của \(\widehat {MAB} \Rightarrow \widehat {MAt} = \widehat {BAt}\)
Ta có: \(At\parallel BC\) nên:
\(\widehat {ABC} = \widehat {BAt}\)(Hai góc so le trong)
\(\widehat {ACB} = \widehat {MAt}\)(Hai góc đồng vị)
Mà \(\widehat {MAt} = \widehat {BAt}\)\( \Rightarrow \widehat {ABC} = \widehat {ACB}\)
Vậy tam giác ABC cân tại A ( Dấu hiệu nhận biết tam giác cân).