Bước 1: Tính tổng các bình phương độ dài hai cạnh của hình chữ nhật. Bước 2. Giải và trình bày phương pháp giải Giải bài 2.11 trang 32 SGK Toán 7 tập 1 – Kết nối tri thức – Bài 6. Số vô tỉ. Căn bậc hai số học. Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài…
Đề bài/câu hỏi:
Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét (làm tròn kết quả đến hàng phần mười)?
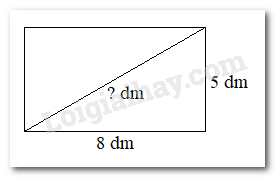
Hướng dẫn:
Bước 1: Tính tổng các bình phương độ dài hai cạnh của hình chữ nhật.
Bước 2: Tìm căn bậc hai số học của tổng vừa tìm được bằng máy tính cầm tay
Bước 3: Làm tròn kết quả đến hàng phần mười.
Lời giải:
Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: \({5^2} + {8^2} = 25 + 64 = 89\)
Độ dài đường chéo của một hình chữ nhật là: \(\sqrt {89} = 9,43398…\)(dm)
Làm tròn kết quả này đến hàng phần mười, ta được: 9,4 dm
Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó