Ta sử dụng định lí cạnh huyền – góc nhọn trong tam giác vuông b) Từ câu a ta chứng minh 2 tam giác AHF. Lời giải Giải Bài 1 trang 84 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài tập cuối chương 8. Cho tam giác ABC cân tại A…
Đề bài/câu hỏi:
Cho tam giác ABC cân tại A (\(\widehat A < {90^o}\)). Hai đường cao BE và CF cắt nhau tại H.
a) Chứng minh rẳng \(\Delta BFC = \Delta CEB\)
b) Chứng minh rằng \(\Delta AEH = \Delta AFH\)
c) Gọi I là trung điểm BC. Chứng minh rằng ba điểm A,H,I thẳng hàng.
Hướng dẫn:
a) Ta sử dụng định lí cạnh huyền – góc nhọn trong tam giác vuông
b) Từ câu a ta chứng minh 2 tam giác AHF = tam giác AHE nhờ những cạnh của 2 tam giác chứng minh được bằng nhau từ câu trên
c) Ta chứng minh AI và AH cùng là phân giác của góc A
Lời giải:
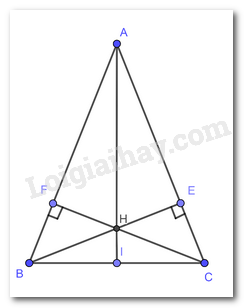
a) Xét \(\Delta BFC\) và \(\Delta CEB\) có:
BC là cạnh chung
\(\widehat B = \widehat C\)(\(\Delta ABC\) cân tại A)
\(\widehat {BEC} = \widehat {CFB} = {90^o}\)
\( \Rightarrow \Delta BFC = \Delta CEB\)(cạnh huyền – góc nhọn )
b) Vì \(\Delta BFC = \Delta CEB \Rightarrow \) BF = EC (2 cạnh tương ứng)
Mà AB = AC (\(\Delta ABC\) cân tại A)
\( \Rightarrow \) AF = AE (AB – BF = AC – EC )
Xét \(\Delta AEH\) và \(\Delta AFH\)ta có :
AF = AE (chứng minh trên)
AH cạnh chung
\(\widehat {HFA} = \widehat {HEA} = {90^o}\)
\( \Rightarrow \Delta AEH = \Delta AFH\)(cạnh huyền – cạnh góc vuông)
c) Vì CF, BE là những đường cao của tam giác ABC và H là giao điểm của chúng
\( \Rightarrow \) H là trực tâm của tam giác ABC
\( \Rightarrow \) AH vuông góc với BC (1)
Xét \(\Delta AIC\) và \(\Delta AIB\) có :
IB = IC (I là trung điểm BC)
AI là cạnh chung
AB = AC ( tam giác ABC cân tại A)
\( \Rightarrow \Delta AIC = \Delta AIB(c – c – c)\)
\( \Rightarrow \widehat {AIC} = \widehat {AIB}\) (2 góc tương ứng) Mà chúng ở vị trí kề bù \( \Rightarrow \widehat {AIC} = \widehat {AIB} = {90^o}\)\( \Rightarrow AI \bot BC\) (2)
Từ (1) và (2) \( \Rightarrow \) A, H, I thẳng hàng.