Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c. Hướng dẫn cách giải/trả lời Giải bài 8 trang 58 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài 2. Tam giác bằng nhau. Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C,…
Đề bài/câu hỏi:
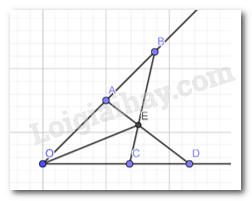
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC
b) \(\Delta EAB=\Delta ECD\)
c) OE là tia phân giác của góc xOy.
Hướng dẫn:
Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g để chứng minh các tam giác bằng nhau rồi suy ra các cạnh tương ứng bằng nhau hoặc các góc tương ứng bằng nhau
Lời giải:
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :
OD = OB
\(\widehat{O}\) chung
OA = OC
\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )
\( \Rightarrow AD = BC\)(2 cạnh tương ứng )
b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)
Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)
Do đó, \(\widehat{BAD}=\widehat{BCD}\)
Vì \(OA+AB=OB; OC+CD=OD\)
Mà \(OC = OA, OD = OB\)
\(\Rightarrow AB=CD\)
Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:
\(\widehat {ABE} = \widehat {CDE}\)
\(AB = CD\)
\(\widehat {BAE} = \widehat {DCE}\)
\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)
c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)
Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :
EB = ED
OB = OD
OE chung
\( \Rightarrow \Delta OBE=\Delta ODE \) (c.c.c)
\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)
\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)