Đáp án Luyện tập – Vận dụng Bài 7. Tam giác cân (trang 94, 95) – SGK Toán 7 Cánh diều. Gợi ý: Chứng minh tam giác AMN cân bằng cách chứng minh hai góc AMN và ANM bằng nhau.
Câu hỏi/Đề bài:
Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC, cắt cạnh AC tại N. Chứng minh tam giác AMN cân.
Hướng dẫn:
Chứng minh tam giác AMN cân bằng cách chứng minh hai góc AMN và ANM bằng nhau.
Lời giải:
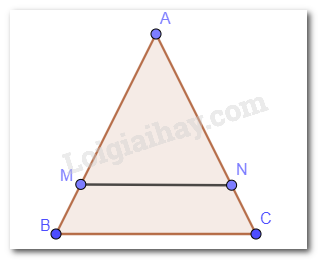
Ta có tam giác ABC cân mà MN // BC. Nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\)(đồng vị)
Mà \(\widehat {ABC} = \widehat {ACB}\)(tam giác ABC cân) nên \(\widehat {AMN} = \widehat {ANM}\).
Vậy tam giác AMN cân tại A ( Tam giác có 2 góc bằng nhau)