Muốn sắp xếp được các đoạn thẳng theo thứ tự tăng dần. Phân tích và giải Giải bài 7 trang 77 SGK Toán 7 tập 2 – Cánh diều – Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác. Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E,…
Đề bài/câu hỏi:
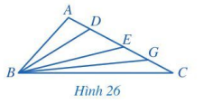
Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E, G sao cho D nằm giữa A và E; E nằm giữa D và G; G nằm giữa E và C (Hình 26). Sắp xếp các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần. Giải thích vì sao?
Hướng dẫn:
Muốn sắp xếp được các đoạn thẳng theo thứ tự tăng dần, ta so sánh chúng với BA và cạnh còn lại trong tam giác tương ứng
Lời giải:
Xét tam giác BAD:
+ Góc A tù (góc > 90°) nên cạnh BD là cạnh lớn nhất trong tam giác này (đối diện với góc A).
Nên BD > BA.
+ Góc A tù nên góc ABD và góc ADB là góc nhọn → góc BDE là góc tù (ba điểm A, D, E thẳng hàng hay góc ADE =180°). Vậy BE (đối diện với góc BDE) > BD.
Tương tự, ta có:
+ Góc BDE là góc tù nên góc DBE và góc DEB là góc nhọn → góc BEG là góc tù. Vậy BG > BE.
+ Góc BEG là góc tù nên góc EBG và góc EGB là góc nhọn → góc BGC là góc tù. Vậy BC > BG.
Vậy BA < BD .
Hay các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần là: BA, BD, BE, BG, BC.