Chứng minh \(\Delta AHB = \Delta AHM\)theo trường hợp c. g. c. Gợi ý giải Giải bài 4 trang 107 SGK Toán 7 tập 2 – Cánh diều – Bài 10. Tính chất ba đường trung tuyến của tam giác. Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G….
Đề bài/câu hỏi:
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
a) \(\Delta AHB = \Delta AHM\); b) \(AG = \dfrac{2}{3}AB\).
Hướng dẫn:
a) Chứng minh \(\Delta AHB = \Delta AHM\)theo trường hợp c.g.c.
b) Dựa vào kết quả chứng minh phần a) và tính chất ba đường trung tuyến trong tam giác để chứng minh.
Lời giải:
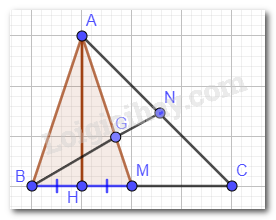
a) Xét tam giác AHB và tam giác AHM có:
AH chung;
\(\widehat {AHB} = \widehat {AHM}\)(H là hình chiếu của A lên BC nên \(AH \bot BC\));
HB = HM (H là trung điểm của BM).
Vậy \(\Delta AHB = \Delta AHM\)(c.g.c).
b) \(\Delta AHB = \Delta AHM\)nên AB = AM ( 2 cạnh tương ứng).
G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC. Nên: \(AG = \dfrac{2}{3}AM\).
Mà AB = AM suy ra: \(AG = \dfrac{2}{3}AB\).