Chứng minh 2 góc ABE và ACF cùng bằng góc A. b) Tính góc FCz (chỉ ra cặp góc đồng vị). Giải và trình bày phương pháp giải Giải bài 3.37 trang 50 sách bài tập toán 7 – Kết nối tri thức với cuộc sống – Ôn tập chương 3. Trong hình 3.37 có…
Đề bài/câu hỏi:
Trong hình 3.37 có \(BE// AC,CF// AB\). Biết \(\widehat A = {80^0};\widehat {ABC} = {60^0}\).
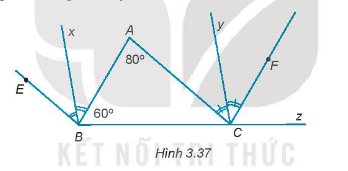
a) Chứng minh rằng \(\widehat {ABE} = \widehat {ACF}.\)
b) Tính số đo của các góc BCF và ACB.
c) Gọi Bx, Cy lần lượt là tia phân giác của các góc ABE và ACF. Chứng minh rằng \(Bx// Cy\).
Hướng dẫn:
a) Chứng minh 2 góc ABE và ACF cùng bằng góc A.
b)
– Tính góc FCz (chỉ ra cặp góc đồng vị).
– Tính góc BCF (Kề bù với góc FCz)
c)
– Tính \(\widehat{ABx}, \widehat{FCy}\).
– Chứng minh \(\widehat{xBC}= \widehat{yCz}\).
Lời giải:
a)
Ta có: \(BE// AC \Rightarrow \widehat {ABE} = \widehat A\) (cặp góc so le trong). Mà \(\widehat A= {80^0}\) nên \(\widehat {ABE} =80^0\)
\(AB//CF \Rightarrow \widehat {ACF} = \widehat A \) (cặp góc so le trong). Mà \(\widehat A= {80^0}\) nên \(\widehat {ACF} =80^0\)
\( \Rightarrow \widehat {ABE} = \widehat {ACF}.\)
b)
Ta có: \(AB// FC \Rightarrow \widehat {zCF} = \widehat {CBA}\) (cặp góc đồng vị). Mà \(\widehat {CBA}= {60^0}\) nên \(\widehat {zCF} =60^0\)
Lại có:\(\widehat {zCF} + \widehat {BCF} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow {60^0} + \widehat {BCF} = {180^0}\\ \Rightarrow \widehat {BCF} = {180^0} – {60^0}\\ \Rightarrow \widehat {BCF} = {120^0}\end{array}\)
Tia AC nằm trong góc BCF nên \(\widehat {ACB} = \widehat {BCF} – \widehat {ACF} = {120^0} – {80^0} = {40^0}\).
c)
Ta có: \(\widehat {EBx} = \widehat {xBA} = \widehat {ACy} = \widehat {yCF} = {40^0}\)
Nên \(\widehat {xBC} = \widehat {xBA} + \widehat {ABC} = {40^0} + {60^0} = {100^0}\)
\(\widehat {yCz} = \widehat {yCF} + \widehat {FCz} = {40^0} + {60^0} = {100^0}\)
\( \Rightarrow \widehat {xBC} = \widehat {yCz}\left( { = {{100}^0}} \right)\)
Mà 2 góc ở vị trí đồng vị nên \(Bx// Cy\) (Dấu hiệu nhận biết hai đường thẳng song song)