Phương pháp phản chứng: giả sử c không cắt b, áp dụng tiên đề Euclid biện luận. Trả lời Giải bài 3.32 trang 46 sách bài tập toán 7 – Kết nối tri thức với cuộc sống – Bài 11: Định lí và chứng minh định lí. Vẽ hình minh hoạ, ghi giả thiết, kết luận bằng kí hiệu và chứng minh định lí sau:…
Đề bài/câu hỏi:
Vẽ hình minh hoạ, ghi giả thiết, kết luận bằng kí hiệu và chứng minh định lí sau:
Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng kia.
Hướng dẫn:
Phương pháp phản chứng: giả sử c không cắt b, áp dụng tiên đề Euclid biện luận.
Lời giải:
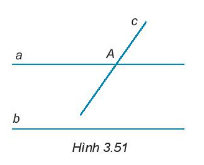
GT: \(a\parallel b\), c cắt a
KL: c cắt b
Chứng minh:
Giả sử c cắt a tại một điểm A.
Nếu c không cắt b thì \(c\parallel b\)nên qua điểm A có 2 đường thẳng song song với b.
Do đó theo tiên đề Euclid, c phải trùng với a (trái giả thiết vì c cắt a)
Vậy không thể có c không cắt b. (đpcm)