Tính \(\widehat {HKB} = {42^o}\) Xét tam giác vuông BHK, \(\widehat {HBK} = {48^o}\. Hướng dẫn trả lời Giải Bài 8 trang 66 sách bài tập toán 7 – Chân trời sáng tạo – Bài tập cuối chương 8. Cho tam giác ABC cân tại A và cho \(\widehat {{A^{}}} = {124^o}\)….
Đề bài/câu hỏi:
Cho tam giác ABC cân tại A và cho \(\widehat {{A^{}}} = {124^o}\). Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC. Tính số đo các góc của tam giác BHK.
Hướng dẫn:
– Tính \(\widehat {HKB} = {42^o}\)
– Xét tam giác vuông BHK, \(\widehat {HBK} = {48^o}\)
Lời giải:
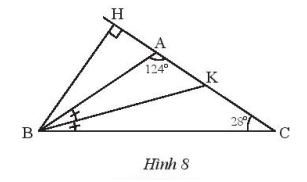
Trong tam giác ABC ta có \(\widehat B = \widehat C = \frac{{{{180}^o} – \widehat {{A^{}}}}}{2} = \frac{{{{180}^o} – {{124}^o}}}{2} = {28^o}\)
Ta có: \(\widehat {HKB} = \widehat {AKB} = {180^o} – {124^o} – {14^o} = {42^o}\)
Trong tam giác vuông BHK ta có: \(\widehat {BHK} = {90^o},\widehat {HBK} = {90^o} – {42^o} = {48^o}\)