Chứng minh: \(\Delta BMH = \Delta CMK\) suy ra \(\widehat B = \widehat C\). Lời giải Giải Bài 4 trang 65 sách bài tập toán 7 – Chân trời sáng tạo – Bài 9: Tính chất ba đường phân giác của tam giác. Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác….
Đề bài/câu hỏi:
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh tam giác ABC là tam giác cân.
Hướng dẫn:
Chứng minh: \(\Delta BMH = \Delta CMK\) suy ra \(\widehat B = \widehat C\)
Lời giải:
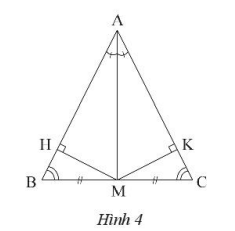
Gọi H và K là chân đường vuông góc kẻ từ M đến AB và AC.
Do AM là tia phân giác của góc BAC nên MH = MK
Xét hai tam giác vuông BMH và CMK có:
Cạnh huyền BM = CM
Cạnh góc vuông: MH = MK
Suy ra: \(\Delta BMH = \Delta CMK\) (cạnh huyền – cạnh góc vuông)
Suy ra: \(\widehat B = \widehat C\)
Vậy tam giác ABC cân tại A.