Đáp án Lời giải Đề thi học kì 1 – Đề số 8 – Đề thi đề kiểm tra Toán lớp 7 Kết nối tri thức.
Câu hỏi/Đề bài:
I. Phần trắc nghiệm (3 điểm)
|
1.D |
2.D |
3.C |
4.A |
5.B |
6.B |
7.A |
8.B |
9.A |
10.B |
Câu 1
Hướng dẫn:
Chỉ tồn tại căn bậc hai số học của số x không âm.
Cách giải:
\(\sqrt x = 4 \Leftrightarrow x = 16\)
Chọn D.
Câu 2
Hướng dẫn:
Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn.
Cách giải:
Gọi số phần trăm học sinh xuất sắc là \(x\% \) (điều kiện: \(x > 0\)). Vì số học sinh xuất sắc bằng số học sinh giỏi nên số phần trăm học sinh giỏi là \(x\% \) (điều kiện: \(x > 0\)).
Ta có:
\(\begin{array}{l}x + x + 63\% + 13\% = 100\% \\2x + 76\% = 100\% \\2x = 100\% – 76\% \\2x = 24\% \\x = 24\% :2\\x = 12\% \end{array}\)
Vậy số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \).
Chọn D.
Câu 3
Hướng dẫn:
Số đối của a là – a
Cách giải:
Số đối của \(\dfrac{{ – 1}}{2}\) là \(\dfrac{1}{2} = – \dfrac{{ – 5}}{{10}}\)
Chọn C.
Câu 4
Hướng dẫn:
\(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,khi\,\,x \ge 0\\ – x\,\,khi\,\,x < 0\end{array} \right.\)
Cách giải:
\(\left| { – 0,55} \right| = 0,55\)
Chọn A.
Câu 5
Hướng dẫn:
So sánh số thập phân thứ 4 với số 5.
Cách giải:
Số thập phân thứ 3 là 2 và số thập phân thứ 4 là số 5 nên kết quả làm tròn bằng 6,672
Chọn B.
Câu 6
Hướng dẫn:
\({a^m}.{a^n} = {a^{m + n}}\)
Cách giải:
\({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3} = {\left( {\dfrac{1}{2}} \right)^{2 + 3}} = {\left( {\dfrac{1}{2}} \right)^5}\)
Chọn B.
Câu 7
Hướng dẫn:
Vận dụng định nghĩa của hai tam giác bằng nhau.
Cách giải:
\(\Delta ABC = \Delta DEF \Rightarrow \angle A = \angle D\) do đó, đáp án A không đúng.
Chọn A.
Câu 8
Hướng dẫn:
Định lý từ vuông góc đến song song
Cách giải:
Vì a và c cùng vuông góc với b nên ta suy ra a // c.
Chọn B.
Câu 9
Hướng dẫn:
Dùng tính chất của tia phân giác
Cách giải:
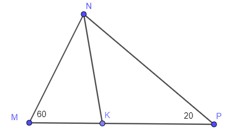
\(\begin{array}{l}\angle MNP = {180^0} – \angle N – \angle P = 180 – 60 – 20 = 100\\ \Rightarrow \angle MNK = 100:2 = 50\\ \Rightarrow \angle MKN = \angle M + \angle MNK = 60 + 50 = 110\end{array}\)
Chọn A.
Câu 10
Hướng dẫn:
Quan sát biểu đồ và xem tỉ lệ gia tăng dân số mỗi năm.
Cách giải:
Tỉ lệ gia tăng dân số Việt Nam năm 1991, 1995, 1999, 2003, 2007 lần lượt là: 1,86%; 1,65%; 1,51%; 1,17%; 1,09%
Ta có 1,86% < 1,65% < 1,51% < 1,17% < 1,09%
Do đó tỉ lệ gia tăng dân số Việt Nam giai đoạn 1991 – 2007 giảm:
1,86% – 1,09% = 0,77%
Chọn B.
II. Phần tự luận (7 điểm)
Câu 1
Hướng dẫn:
Áp dụng tính toán theo thứ tự thực hiện phép tính.
Cách giải:
a. \(\dfrac{2}{7} + \left( {\dfrac{{ – 17}}{7}} \right) + \dfrac{8}{7}\)\( = \dfrac{{2 + ( – 17) + 8}}{7} = \dfrac{{ – 7}}{7} = – 1\)
b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} – \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} – \dfrac{2}{3}} \right) = \dfrac{5}{9}:\dfrac{{ – 3}}{{22}} + \dfrac{5}{9}:\dfrac{{ – 3}}{5} = \dfrac{5}{9}.\dfrac{{ – 22}}{3} + \dfrac{5}{9}.\dfrac{{ – 5}}{3}\)
\( = \left( {\dfrac{{ – 22}}{3} + \dfrac{{ – 5}}{3}} \right).\dfrac{5}{9} = ( – 9).\dfrac{5}{9} = – 5\)
c. \(\dfrac{{{{\left( { – 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} – 1} \right| + {2023^0} = \dfrac{{ – 8}}{5}.\left| {\dfrac{{ – 3}}{4}} \right| + 1\)\( = \dfrac{{ – 8}}{5}.\dfrac{3}{4} + 1 = \dfrac{{ – 6}}{5} + 1 = \dfrac{{ – 1}}{5}\)
d. \( – \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}} – {2^2}.\left| { – \dfrac{1}{4}} \right|\)=\( – \dfrac{5}{2}.\dfrac{3}{5} – 4.\dfrac{1}{4}\)=\( – \dfrac{3}{2} – 1\)=\( – \dfrac{5}{2}\)
Câu 2
Hướng dẫn:
\(\left| x \right| = a\,\) với \((a > 0)\)\( \Leftrightarrow \left[ \begin{array}{l}x = a\\x = – a\end{array} \right.\)
\({x^2} = a\,\)với \((a > 0)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \sqrt a \\x = – \sqrt a \end{array} \right.\)
Cách giải:
a. \(x + 1\dfrac{1}{2} = – 5,6 \Leftrightarrow x + 1,5 = – 5,6 \Leftrightarrow x = – 5,6 – 1,5 \Leftrightarrow x = \, – 7,1\)
b. \(\,\,\left| {x – \dfrac{1}{4}} \right| = \dfrac{5}{4} \Rightarrow \left[ \begin{array}{l}x – \dfrac{1}{4} = \dfrac{5}{4}\\x – \dfrac{1}{4} = – \dfrac{5}{4}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{2}\\x\,\,\,\,\,\,\,\,\,\,\, = – 1\end{array} \right.\)
c. \({\left( {\dfrac{1}{5} – \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4} \Rightarrow \left[ \begin{array}{l}\dfrac{1}{5} – \dfrac{3}{2}x = \dfrac{3}{2}\\\dfrac{1}{5} – \dfrac{3}{2}x = \dfrac{{ – 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{1}{5} – \dfrac{3}{2}\\\dfrac{3}{2}x = \dfrac{1}{5} – \dfrac{{ – 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{{ – 13}}{{10}}\\\dfrac{3}{2}x = \dfrac{{17}}{{10}}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{{ – 13}}{{15}}\\x = \dfrac{{17}}{{15}}\end{array} \right.\)
Câu 3
Hướng dẫn:
1) Chứng minh \(\Delta BAM = \Delta BNM\left( {c.g.c} \right)\)
2) Chứng minh \(BM\) là đường trung trực của đoạn thẳng \(AN\)
Mà \(I\) là giao điểm của \(BM\) và \(AN\) nên \(I\) là trung điểm của \(AN\).
3) *Chứng minh \(\angle MNC = {90^0}\)
Ta có: \(\left\{ \begin{array}{l}\angle ABC + \angle ACB = \angle BAC = {90^0}\\\angle MCN + \angle CMN = \angle MNC = {90^0}\end{array} \right.\), suy ra \(\angle ABC = \angle CMN\) (đpcm)
*Chứng minh \(\Delta MAK = \Delta MNC\left( {c.g.c} \right) \Rightarrow \angle AMK = \angle CMN\)
\( \Rightarrow \angle AMN + \angle AMK = {180^0}\)
Do đó, \(K,M,N\) là ba điểm thẳng hàng.
Cách giải:
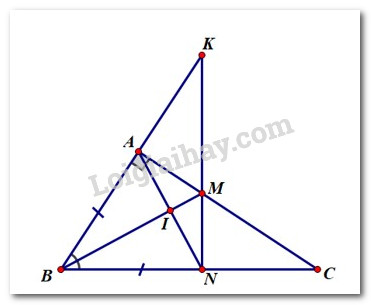
1) Vì \(BM\) là phân giác của \(\angle ABC \Rightarrow \angle ABM = \angle NBM\)
Xét \(\Delta BAM\) và \(\Delta BNM\) có:
\(\left. \begin{array}{l}AB = BN\left( {gt} \right)\\\angle ABM = \angle NBM\left( {cmt} \right)\\BM\,\,chung\end{array} \right\} \Rightarrow \Delta BAM = \Delta BNM\left( {c.g.c} \right)\)
2) \(\Delta BAM = \Delta BNM\left( {cmt} \right) \Rightarrow AM = MN\) (hai cạnh tương ứng)
Ta có: \(AB = BN\left( {gt} \right)\) và \(AM = MN\left( {cmt} \right)\)
\( \Rightarrow BM\) là đường trung trực của đoạn thẳng \(AN\)
Mà \(I\) là giao điểm của \(BM\) và \(AN\) nên \(I\) là trung điểm của \(AN\).
3) *\(\Delta ABC\) vuông tại \(A\left( {gt} \right) \Rightarrow \angle BAC = {90^0}\) hay \(\angle BAM = {90^0}\)
\(\Delta BAM = \Delta BNM\left( {cmt} \right) \Rightarrow \angle BAM = \angle BNM = {90^0}\)
Hai góc \(\angle BNM\) và \(\angle MNC\) kề bù nhau nên \(\angle MNC = {180^0} – {90^0} = {90^0}\)
Ta có: \(\left\{ \begin{array}{l}\angle ABC + \angle ACB = \angle BAC = {90^0}\\\angle MCN + \angle CMN = \angle MNC = {90^0}\end{array} \right.\), suy ra \(\angle ABC = \angle CMN\) (đpcm)
*Xét \(\Delta MAK\) và \(\Delta MNC\) có:
\(\left. \begin{array}{l}AM = MN\left( {cmt} \right)\\\angle KAM = \angle MNC = {90^0}\\AK = NC\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta MAK = \Delta MNC\left( {c.g.c} \right) \Rightarrow \angle AMK = \angle CMN\) (hai góc tương ứng)
Ta có: \(\angle AMN + \angle CMN = {180^0}\) mà \(\angle CMN = \angle AMK\left( {cmt} \right)\)
\( \Rightarrow \angle AMN + \angle AMK = {180^0}\)
Do đó, \(K,M,N\) là ba điểm thẳng hàng.
Câu 4
Hướng dẫn:
Đưa về lũy thừa cùng cơ số hoặc cùng số mũ để so sánh.
Cách giải:
Ta có: \({4^{30}} = {2^{30}}{.2^{30}} = {\left( {{2^3}} \right)^{30}}.{\left( {{2^2}} \right)^{15}} > {8^{10}}{.3^{15}} > \left( {{8^{10}}{{.3}^{10}}} \right).3 > {24^{10}}.3\)
Vậy \({2^{30}} + {3^{30}} + {4^{30}}\) > \({3.24^{10}}\).