Giải chi tiết Lời giải Đề thi học kì 1 – Đề số 5 – Đề thi đề kiểm tra Toán lớp 7 Kết nối tri thức.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm
|
1.D |
2.D |
3.B |
4.B |
5.B |
6.B |
7.B |
8.B |
9.A |
10.C |
Câu 1
Hướng dẫn:
Tìm \(x\) biết căn bậc hai số học của nó bằng \(a\).
Tính \({x^2}\)
Cách giải:
\(\sqrt x = 3 \Rightarrow x = {3^2} = 9 \Rightarrow {x^2} = {9^2} = 81.\)
Chọn D.
Câu 2
Hướng dẫn:
Rút gọn các phân số về dạng tối giản.
Cách giải:
Ta có: \(\dfrac{{ – 24}}{{30}} = \dfrac{{ – 24:( – 6)}}{{30:( – 6)}} = \dfrac{4}{{ – 5}}\)
Chọn D.
Câu 3
Hướng dẫn:
*Làm tròn theo quy tắc làm tròn số thập phân dương:
– Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
– Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
*Muốn làm tròn số thập phân âm, ta làm tròn số thập phân dương rồi lấy số đối của kết quả vừa làm tròn.
Cách giải:
Trước tiên, ta làm tròn số 2,13513 đến chữ số thập phân thứ hai được: 2,14 ( do chữ số ở hàng làm tròn là 3, chữ số ngay bên phải hàng làm tròn là \(5 \ge 5\) nên ta cộng thêm 1 đơn vị vào hàng làm tròn, bỏ đi các chữ số bên phải hàng làm tròn).
Do đó, làm tròn -2,13513 đến chữ số thập phân thứ hai, ta được -2,14.
Chọn B.
Câu 4
Hướng dẫn:
Số đo góc ngoài tam giác bằng tổng số đo 2 góc trong không kề với nó.
Cách giải:
Số đo góc ngoài tại đỉnh C là: \(60^\circ + 55^\circ = 115^\circ \)
Chọn B.
Câu 5
Hướng dẫn:
2 tam giác có 2 cặp góc tương ứng và cặp cạnh xen giữa bằng nhau thì hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
Cách giải:
Cạnh BC xen giữa góc B và góc C; cạnh PN xen giữa góc P và góc N. Mà \(\widehat P = \widehat C\) nên để 2 tam giác bằng nhau theo trường hợp góc – cạnh – góc thì cần thêm điều kiện \(\widehat B = \widehat N\).
Chọn B.
Câu 6
Hướng dẫn:
Tổng số đo 3 góc trong tam giác là 180 độ.
Tam giác cân có 2 góc ở đáy bằng nhau.
Cách giải:
Tam giác cân có 2 góc ở đáy bằng \(52^\circ \)nên góc ở đỉnh là: \(180^\circ – 52^\circ – 52^\circ = 76^\circ \).
Chọn B
Câu 7
Hướng dẫn:
– Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau.
– Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt đường thẳng phân biệt ab, và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng hai thì a và b song song với nhau.
– Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì sẽ vuông góc với đường thẳng còn lại.
Cách giải:
Ta có \(\angle ABD = {90^o}\left( {gt} \right) \Rightarrow AB \bot BD\)
Mà \(AE\,//\,BD\,\left( {gt} \right)\)
\( \Rightarrow AE \bot AB \Rightarrow \angle BAE = {90^o}\)
Vì \(AE\,//\,BD \Rightarrow \angle EDx = \angle AED = {55^o}\) (đối đỉnh)
Mà \(\angle BDE + \angle EDx = {180^o}\) (hai góc kề bù)
\( \Rightarrow \angle BDE = {180^o} – {55^o} = {125^o}\)
Chọn B.
Câu 8
Hướng dẫn:
Sử dụng tính chất phân phối của phép nhân và phép nhân.
Cách giải:
\(\begin{array}{l}B = \left( { – \dfrac{3}{9}} \right).\dfrac{3}{{11}} – \dfrac{6}{9}.\dfrac{3}{{11}}\\\,\,\,\,\, = \left( {\dfrac{{ – 1}}{3}} \right).\dfrac{3}{{11}} + \left( {\dfrac{{ – 2}}{3}} \right).\dfrac{3}{{11}}\end{array}\)
\(\begin{array}{l}\,\,\,\,\, = \dfrac{3}{{11}}.\left( {\dfrac{{ – 1}}{3} + \dfrac{{ – 2}}{3}} \right)\\\,\,\,\,\, = \dfrac{3}{{11}}.\left( { – 1} \right) = \dfrac{{ – 3}}{{11}}\end{array}\)
Chọn B.
Câu 9
Hướng dẫn:
Đưa các số thập phân về dạng phân số theo các quy tắc đã học rồi tìm \(x\).
Chú ý: \(0,\left( 1 \right) = \dfrac{1}{9}\)
Cách giải:
Ta có:
\(\begin{array}{l}\dfrac{{12}}{{40}} – 2x = 0,\left( 1 \right) + {\left[ {1,\left( {24} \right)} \right]^0}\\\dfrac{3}{{10}} – 2x = \dfrac{1}{9} + 1\\\dfrac{3}{{10}} – 2x = \dfrac{{10}}{9}\\2x = \dfrac{3}{{10}} – \dfrac{{10}}{9}\\2x = \dfrac{{ – 73}}{{90}}\\x = \dfrac{{ – 73}}{{90}}:2\\x = \dfrac{{ – 73}}{{180}}\end{array}\)
Vậy \(x = \dfrac{{ – 73}}{{180}}\).
Chọn A.
Câu 10
Hướng dẫn:
Dựa vào biểu đồ đoạn thẳng, ta có thể xác định xu hướng tăng hoặc giảm của số liệu trong một khoảng thời gian nhất định.
Cách giải:
Nhu cầu bán máy tính để bàn giảm mạnh trong 6 tháng, nhu cầu bán máy tính xách tay tăng mạnh trong 6 tháng.
Chọn C.
Phần II. Tự luận:
Bài 1
Hướng dẫn:
a), b) Thực hiện phép cộng, trừ, nhân, chia với số hữu tỉ
Vận dụng tính chất phân phối của phép nhân và phép cộng tính hợp lí
c) Tích và thương của hai lũy thừa cùng cơ số:
+ Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
+ Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m – n}}\,\left( {x \ne 0;m \ge n} \right)\)
Lũy thừa của một lũy thừa:
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Cách giải:
a) \(1\dfrac{3}{4}.\dfrac{{ – 16}}{7} = \dfrac{7}{4}.\dfrac{{ – 16}}{7} = – 4\)
b) \(12:\dfrac{{ – 6}}{5} + \dfrac{1}{5} = 12.\dfrac{{ – 5}}{6} + \dfrac{1}{5} = – 10 + 0,2 = – 9,8\)
c)
\(\dfrac{2}{{{3^2}}} + \dfrac{1}{3}:\left( {\dfrac{{ – 3}}{2}} \right) + \sqrt {\dfrac{1}{4}} .\left( { – 0,5} \right) = \dfrac{2}{9} + \dfrac{1}{3}.\dfrac{{ – 2}}{3} + \dfrac{1}{2}.\dfrac{{ – 1}}{2} = \dfrac{2}{9} + \dfrac{{ – 2}}{9} + \dfrac{{ – 1}}{4} = \dfrac{{ – 1}}{4}\)
d)
\({\left( {0,1} \right)^{21}}:{\left( { – 0,01} \right)^{10}} = {\left( {0,1} \right)^{21}}:{\left( {0,01} \right)^{10}} = {\left( {0,1} \right)^{21}}:{\left[ {{{\left( {0,1} \right)}^2}} \right]^{10}} = {\left( {0,1} \right)^{21}}:{\left( {0,1} \right)^{20}} = 0,1\)
Bài 2
Hướng dẫn:
a) + b) Thực hiện các phép toán với số hữu tỉ.
c) Đưa phương trình về dạng: \(\left| {f\left( x \right)} \right| = a\left( {a \ge 0} \right)\)
+ Trường hợp 1: \(f\left( x \right) = a\)
+ Trường hợp 2: \(f\left( x \right) = – a\)
d) Vận dụng định nghĩa hai phân thức bằng nhau.
Cách giải:
a) \(x – \dfrac{2}{5} = \dfrac{{ – 9}}{{10}}\)
\(\begin{array}{l}x = \dfrac{{ – 9}}{{10}} + \dfrac{2}{5}\\x = \dfrac{{ – 9 + 2.2}}{{10}}\\x = \dfrac{{ – 5}}{{10}} = \dfrac{{ – 1}}{2}\end{array}\)
Vậy \(x = – \dfrac{1}{2}\)
b) \(\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ – 5}}{6}\)
\(\begin{array}{l}\dfrac{1}{4}x = \dfrac{{ – 5}}{6} – \dfrac{3}{4}\\\dfrac{1}{4}x = \dfrac{{ – 5.2 – 3.3}}{{12}}\\\dfrac{1}{4}x = \dfrac{{ – 19}}{{12}}\\x = \dfrac{{ – 19}}{{12}}:\dfrac{1}{4}\\x = \dfrac{{ – 19}}{3}\end{array}\)
Vậy \(x = \dfrac{{ – 19}}{3}\)
c) \(\left| {x + \dfrac{1}{2}} \right| – \dfrac{1}{3} = 0\)
\(\left| {x + \dfrac{1}{2}} \right| = \dfrac{1}{3}\)
Trường hợp 1: \(x + \dfrac{1}{2} = \dfrac{1}{3} \Rightarrow x = \dfrac{1}{3} – \dfrac{1}{2} = \dfrac{{ – 1}}{6}\)
Trường hợp 2: \(x + \dfrac{1}{2} = \dfrac{{ – 1}}{3} \Rightarrow x = \dfrac{{ – 1}}{3} – \dfrac{1}{2} = \dfrac{{ – 5}}{6}\)
Vậy \(x \in \left\{ {\dfrac{{ – 1}}{6};\dfrac{{ – 5}}{6}} \right\}\)
Bài 3
Hướng dẫn:
a) Sử dụng trường hợp bằng nhau cạnh – cạnh – cạnh để chứng minh hai tam giác đó bằng nhau.
b) Chứng minh tam giác bằng nhau, từ đó suy ra các cạnh tương ứng bằng nhau.
Cách giải:
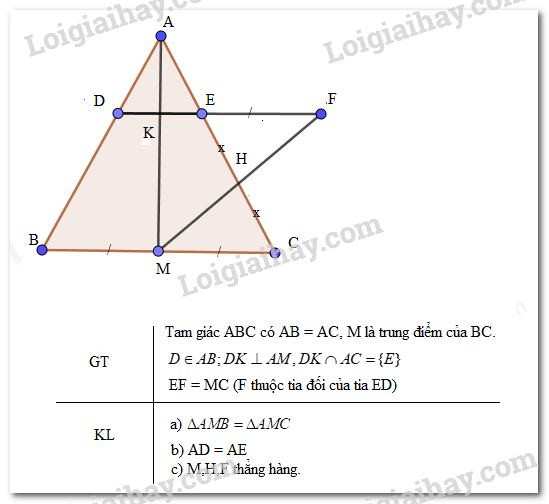
a) Xét \(\Delta AMB\) và \(\Delta AMC\)có:
MB = MC (gt)
AM chung
AB = AC (gt)
\( \Rightarrow \Delta AMB = \Delta AMC(c.c.c)\)
b) Vì \(\Delta AMB = \Delta AMC(cmt) \Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)
Xét \(\Delta ADK\) và \(\Delta AEK\)có:
\(\widehat {AKD} = \widehat {AKE}( = 90^\circ )\)
AK chung
\(\widehat {DAK} = \widehat {EAK}(cmt)\)
\( \Rightarrow \Delta ADK = \Delta AEK(g.c.g)\)
Do đó, AD = AE (2 cạnh tương ứng)
c) Vì \(\Delta AMB = \Delta AMC(cmt) \Rightarrow \widehat {BMA} = \widehat {CMA}\)(2 góc tương ứng)
Mà \(\widehat {BMA} + \widehat {CMA} = 180^\circ \) (2 góc kề bù)
\(\widehat {BMA} = \widehat {CMA} = 90^\circ \Rightarrow AM \bot BC\)
Mà \(AM \bot DE(gt)\)
\( \Rightarrow DE//BC\).
\( \Rightarrow \widehat {HEF} = \widehat {HCM}\) (2 góc so le trong)
Xét \(\Delta HEF\) và \(\Delta HCM\)có:
EF = CM (gt)
\(\widehat {HEF} = \widehat {HCM}(cmt)\)
HE = HC (gt)
\( \Rightarrow \Delta HEF = \Delta HCM(c.g.c)\)
\( \Rightarrow \widehat {FHE} = \widehat {MHC}\) (2 góc tương ứng)
Mà \(\widehat {FHE} + \widehat {FHC} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {MHC} + \widehat {FHC} = 180^\circ \)
Do đó, M,H,F thẳng hàng.
Bài 5
Hướng dẫn:
Để \(P = \dfrac{{M\left( x \right)}}{{n\left( x \right)}}\) có giá trị nguyên
+ Bước 1: Biến đổi \(P = m\left( x \right) + \dfrac{k}{{n\left( x \right)}}\). Trong đó \(k\) là số nguyên
+ Bước 2: Lập luận: Để \(P\) có giá trị nguyên thì \(k \vdots n\left( x \right)\) hay \(n\left( x \right) \in U\left( k \right)\)
+ Bước 3: Lập bảng giá trị và kiểm tra \(x\) với điều kiện đã tìm
+ Bước 4: Kết luận.
Cách giải:
Điều kiện: \(x \ne 2\).
Ta có:
\(M = \dfrac{{5 – x}}{{x – 2}} = \dfrac{{3 – (x – 2)}}{{x – 2}} = \dfrac{3}{{x – 2}} – 1\)
M nhỏ nhất \( \Leftrightarrow \dfrac{3}{{x – 2}}\) nhỏ nhất
\( \Leftrightarrow x – 2\) lớn nhất và x – 2 < 0.
\( \Leftrightarrow x\) lớn nhất và x < 2.
\( \Leftrightarrow x = 1\) (vì x nguyên)
Vậy giá trị nhỏ nhất của M là: min M = \(\dfrac{3}{{1 – 2}} – 1 = – 4\) khi x = 1.