Giải Lời giải Đề thi học kì 1 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 7 Kết nối tri thức.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm
|
1.B |
2.D |
3.C |
4.D |
5.A |
6.B |
7.C |
8.B |
9.B |
10.D |
Câu 1
Hướng dẫn:
Số hữu tỉ và số hữu tỉ được gọi chung là số thực.
Số hữu tỉ là số được viết dưới dạng phân số \(\frac{a}{b}\,\) với \(a,b \in \mathbb{Z},b \ne 0\).
Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.
Cách giải:
+ Mọi số vô tỉ đều là số thực là phát biểu đúng.
+ Mọi số thực đều là số vô tỉ là phát biểu sai.
+ Số 0 là số hữu tỉ là phát biểu đúng.
+ \( – \sqrt 2 \) là số vô tỉ là phát biểu đúng.
Chọn B.
Câu 2
Hướng dẫn:
Diện tích của tam giác có cạnh là \(a\) và chiều cao tương ứng với cạnh đó là \(h\) được tính theo công thức \(S = \frac{1}{2}a.h\)
Cách giải:
Chiều cao của tam giác là: \(\frac{2}{9}:2 = \frac{2}{9}.\frac{1}{2} = \frac{1}{9}\,\left( m \right)\)
Diện tích của tam giác là: \(\frac{1}{2}.\frac{2}{9}.\frac{1}{9} = \frac{1}{{81}}\,\left( {{m^2}} \right)\)
Vậy diện tích của tam giác đã cho là \(\frac{1}{{81}}{m^2}\)
Chọn D.
Câu 3
Hướng dẫn:
Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ – x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
Ta có: \(6 = \sqrt {36} \)
Vì \(36 > 34\) nên \(\sqrt {36} > \sqrt {34} \) suy ra \(\sqrt {36} – \sqrt {34} > 0\) hay \(6 – \sqrt {34} > 0\)
Do đó, \(\left| {6 – \sqrt {34} } \right| = 6 – \sqrt {34} \)
Ta có:
\(\begin{array}{l}\left| {6 – \sqrt {34} } \right| + 3 + \sqrt {34} \\ = 6 – \sqrt {34} + 3 + \sqrt {34} \\ = \left( {6 + 3} \right) + \left( { – \sqrt {34} + \sqrt {34} } \right)\\ = 9 + 0\\ = 9\end{array}\)
Chọn C.
Câu 4
Hướng dẫn:
Thực hiện phép nhân số hữu tỉ.
Vận dụng quy tắc làm tròn số:
Khi làm tròn một số thập phân đến hàng nào thì hàng đó gọi là hàng quy tròn.
Muốn làm tròn số thập phân đến một hàng quy tròn nào đó, ta thực hiện các bước sau:
– Gạch dưới chữ số thập phân của hàng quy tròn.
– Nhìn sang chữ số ngay bên phải:
+ Nếu chữ số đó lớn hơn hoặc bằng 5 thì tăng chữ số gạch dưới lên một đơn vị rồi thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân.
+ Nếu chữ số đó nhỏ hơn 5 thì giữ nguyên chữ số gạch chân dưới và thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúcng ở phần thập phân.
Cách giải:
Độ dài đường chéo của màn hình là: \(36.2,54 = 91,44\,\left( {cm} \right) \approx 91,4\,\left( {cm} \right)\)
Chọn D.
Câu 5
Hướng dẫn:
Áp dụng tính chất tổng ba góc của một tam giác \(\widehat A + \widehat B + \widehat C = {180^0}\) để tính số đo góc \(\widehat {B.}\)
Cách giải:
Xét tam giác ABC có :\(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B = {180^0} – \left( {\widehat A + \widehat C} \right) = {180^0} – \left( {{{98}^0} + {{52}^0}} \right) = {30^0}\).
Chọn A
Câu 6
Hướng dẫn:
Sử dụng tính chất tổng ba góc của một tam giác và sử dụng tính chất của tam giác cân (tam giác cân có hai góc ở đáy bằng nhau).
Cách giải:
Giả sử ta có \(\Delta ABC\) cân tại \(A \Rightarrow \widehat B = \widehat C.\) (tính chất tam giác cân)
Mà \(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B = \widehat C = \frac{{{{180}^0} – \widehat A}}{2} = \frac{{{{180}^0} – {{52}^0}}}{2} = {64^0}.\)
Chọn B
Câu 7
Hướng dẫn:
Hai góc kề bù có tổng số đo góc bằng \({180^0}\)
Vận dụng tính chất tia phân giác của một góc: \(Ot\) là tia phân giác của \(\angle xOy \Rightarrow \angle xOt = \angle yOt = \frac{1}{2}\angle xOy\)
Cách giải:
Theo giả thiết: \(\angle AOC – \angle BOC = {68^0} \Rightarrow \angle AOC = \angle BOC + {68^0}\)
Vì \(\angle AOC\) và \(\angle BOC\) là hai góc kề bù nên \(\angle AOC + \angle BOC = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle BOC + {68^0} + \angle BOC = {180^0}\\ \Rightarrow 2\angle BOC = {180^0} – {68^0}\\ \Rightarrow 2\angle BOC = {112^0}\\ \Rightarrow \angle BOC = {112^0}:2\\ \Rightarrow \angle BOC = {56^0}\end{array}\)
Vì \(Ot\) là tia phân giác của góc \(BOC\) nên \(\angle BOt = \frac{1}{2}\angle BOC\) (tính chất tia phân giác của một góc)
\( \Rightarrow \angle BOt = \frac{1}{2}{.56^0} = {28^0}\)
Vậy \(\angle BOt = {28^0}\)
Chọn C.
Câu 8
Hướng dẫn:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song với nhau thì hai góc đồng vị bằng nhau.
Hai góc kề bù có tổng số đo góc bằng \({180^0}\).
Cách giải:
*Ta có: \(m\) và \(n\) song song với nhau nên \(\angle mAB = \angle {B_3} = {80^0}\) (hai góc đồng vị)
*Hai góc \({B_3}\) và góc \({B_4}\) kề bù với nhau nên \(\angle {B_3} + \angle {B_4} = {180^0}\)
\(\begin{array}{l} \Rightarrow {80^0} + \angle {B_4} = {180^0}\\ \Rightarrow \angle {B_4} = {180^0} – {80^0} = {100^0}\end{array}\)
Chọn B.
Câu 9
Hướng dẫn:
Ứng dụng của biểu đồ hình quạt tròn.
Cách giải:
Biểu đồ hình quạt tròn dùng để so sánh các thành phần trong toàn bộ dữ liệu.
Chọn B.
Câu 10
Hướng dẫn:
Phân tích dữ liệu biểu đồ đoạn thẳng.
Cách giải:
Từ biểu đồ đoạn thẳng, ta thấy năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm.
Chọn D.
Phần II. Tự luận:
Bài 1
Hướng dẫn:
a), b) Thực hiện phép cộng, trừ, nhân, chia với số hữu tỉ
Vận dụng tính chất phân phối của phép nhân và phép cộng tính hợp lí
c) Tích và thương của hai lũy thừa cùng cơ số:
+ Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
+ Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m – n}}\,\left( {x \ne 0;m \ge n} \right)\)
Lũy thừa của một lũy thừa:
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Cách giải:
a) \(\frac{{ – 15}}{{14}}:\frac{{17}}{{23}} – \frac{{15}}{{14}}:\frac{{17}}{{11}} – \frac{6}{7}\)
\(\begin{array}{l} = \frac{{ – 15}}{{14}}.\frac{{23}}{{17}} – \frac{{15}}{{14}}.\frac{{11}}{{17}} – \frac{6}{7}\\ = \frac{{ – 15}}{{14}}.\frac{{23}}{{17}} + \frac{{ – 15}}{{14}}.\frac{{11}}{{17}} – \frac{6}{7}\\ = \frac{{ – 15}}{{14}}.\left( {\frac{{23}}{{17}} + \frac{{11}}{{17}}} \right) – \frac{6}{7}\\ = \frac{{ – 15}}{{14}}.\frac{{34}}{{17}} – \frac{6}{7}\\ = \frac{{ – 15}}{{14}}.2 – \frac{6}{7}\\ = \frac{{ – 15}}{7} – \frac{6}{7}\\ = \frac{{ – 21}}{7} = – 3\end{array}\)
b) \(\left( {\frac{{ – 5}}{3} + \frac{{ – 3}}{2}} \right):\frac{{17}}{{13}} + \left( {\frac{7}{2} + \frac{{ – 1}}{3}} \right):\frac{{17}}{{13}}\)
\(\begin{array}{l} = \left( {\frac{{ – 5}}{3} + \frac{{ – 3}}{2}} \right).\frac{{13}}{{17}} + \left( {\frac{7}{2} + \frac{{ – 1}}{3}} \right).\frac{{13}}{{17}}\\ = \frac{{13}}{{17}}.\left( {\frac{{ – 5}}{3} + \frac{{ – 3}}{2} + \frac{7}{2} + \frac{{ – 1}}{3}} \right)\\ = \frac{{13}}{{17}}.\left[ {\left( {\frac{{ – 5}}{3} + \frac{{ – 1}}{3}} \right) + \left( {\frac{{ – 3}}{2} + \frac{7}{2}} \right)} \right]\\ = \frac{{13}}{{17}}.\left( {\frac{{ – 6}}{3} + \frac{4}{2}} \right)\\ = \frac{{13}}{{17}}.\left( { – 2 + 2} \right)\\ = \frac{{13}}{{17}}.0 = 0\end{array}\)
c) \({3^2}.\frac{1}{{243}}{.81^2}.\frac{1}{{{3^3}}}\)
\(\begin{array}{l} = {3^2}.\frac{1}{{{3^5}}}.{\left( {{3^4}} \right)^2}.\frac{1}{{{3^3}}}\\ = {3^2}.\frac{1}{{{3^5}}}{.3^8}.\frac{1}{{{3^3}}}\\ = \frac{{{3^2}{{.3}^8}}}{{{3^5}{{.3}^3}}} = \frac{{{3^{2 + 8}}}}{{{3^{5 + 3}}}}\\ = \frac{{{3^{10}}}}{{{3^8}}} = {3^{10 – 8}} = {3^2} = 9\end{array}\)
d) \(\left( {{{4.2}^5}} \right):\left( {{2^3}.\frac{1}{{16}}} \right)\)
\(\begin{array}{l} = \left( {{2^2}{{.2}^5}} \right):\left( {{2^3}.\frac{1}{{{2^4}}}} \right)\\ = {2^{2 + 5}}:\frac{{{2^3}}}{{{2^4}}} = {2^7}:\frac{1}{2}\\ = {2^7}.2 = {2^{7 + 1}}\\ = {2^8} = 256\end{array}\)
Bài 2
Hướng dẫn:
a) Vận dụng quy tắc chuyển vế tìm \(x\)
b) \(A\left( x \right).B\left( x \right) = 0\)
Trường hợp 1: Giải \(A\left( x \right) = 0\)
Trường hợp 2: Giải \(B\left( x \right) = 0\)
c) Tính căn bậc hai
Vận dụng quy tắc chuyển vế tìm \(x\)
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ – x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(\left( { – 0,2} \right) – x.\frac{1}{6} = \frac{2}{3}\)
\(\begin{array}{l}\frac{{ – 1}}{5} – x.\frac{1}{6} = \frac{2}{3}\\ – x.\frac{1}{6} = \frac{2}{3} – \frac{{ – 1}}{5}\\ – x.\frac{1}{6} = \frac{{10}}{{15}} + \frac{3}{{15}}\\ – x.\frac{1}{6} = \frac{{13}}{{15}}\\ – x = \frac{{13}}{{15}}:\frac{1}{6} = \frac{{13}}{{15}}.6\\ – x = \frac{{26}}{5}\\x = \frac{{ – 26}}{5}\end{array}\)
Vậy \(x = \frac{{ – 26}}{5}\)
b) \(5.\left( {\frac{1}{{\sqrt {25} }} – x} \right) – \sqrt {\frac{1}{{81}}} = \frac{{ – 1}}{9}\)
\(\begin{array}{l}5.\left( {\frac{1}{5} – x} \right) – \frac{1}{9} = \frac{{ – 1}}{9}\\5.\left( {\frac{1}{5} – x} \right) = \frac{{ – 1}}{9} + \frac{1}{9}\\5.\left( {\frac{1}{5} – x} \right) = 0\\\frac{1}{5} – x = 0\\x = \frac{1}{5}\end{array}\)
Vậy \(x = \frac{1}{5}\)
c) \(\left| x \right| = \frac{{13}}{{17}}\)
\(x = \frac{{13}}{{17}}\) hoặc \(x = \frac{{ – 13}}{{17}}\)
Vậy \(x \in \left\{ {\frac{{13}}{{17}};\frac{{ – 13}}{{17}}} \right\}\)
Bài 3
Hướng dẫn:
+ Sử dụng trường hợp bằng nhau cạnh huyền – góc nhọn để chứng minh hai tam giác vuông đó bằng nhau
+ Từ cặp tam giác bằng nhau ở ý a) ta suy ra hai cạnh tương ứng bằng nhau, từ đó chứng minh được tam giác ABE cân, kết hợp với điều kiện góc \(\widehat B = 60^\circ \) ta kết luận được tam giác này đều.
+ Ta đi chứng minh tam giác AEC cân tại E vì có hai góc ở đáy bằng nhau; từ đó suy ra hai cạnh bên bằng nhau để tính được độ dài cạnh EC; tính BC bằng cách \(BC = BE + EC\) .
Cách giải:
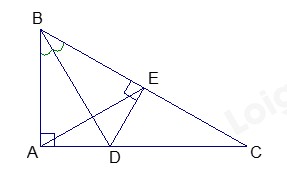
a) Chứng minh: \(\Delta \)ABD = \(\Delta \)EBD
Xét \(\Delta \)ABD và \(\Delta \)EBD, có:
\(\widehat {BAD} = \widehat {BED} = {90^0}(gt)\)
BD là cạnh huyền chung
\(\widehat {ABD} = \widehat {EBD}(gt)\)
Vậy \(\Delta ABE = \Delta EBD\) (cạnh huyền – góc nhọn)
b) Chứng minh: \(\Delta \)ABE là tam giác đều.
Ta có: \(\Delta ABE = \Delta EBD\)(cmt)\( \Rightarrow \)AB = EB (hai cạnh tương ứng).
Do đó \(\Delta \)ABE cân tại B.
Mà \(\widehat B = {60^0}\) (gt) nên \(\Delta ABE\) đều. (dhnb)
c) Tính độ dài cạnh BC
Ta có: \(\widehat {EAC} + \widehat {BEA} = {90^0}\)(gt)
\(\widehat C + \widehat B = {90^0}\) (\(\Delta \)ABC vuông tại A)
Mà \(\widehat {BEA} = \widehat B = {60^0}\) (\(\Delta \)ABE đều) nên \(\widehat {EAC} = \widehat C\)\( \Rightarrow \) \(\Delta \)AEC cân tại E
\( \Rightarrow EA = EC\) mà \(EA = AB = EB = 5cm\)
Do đó EC = 5cm
Vậy BC = EB + EC = 5cm + 5cm = 10cm.
Bài 4:
Hướng dẫn:
+ Nếu một đường thẳng cắt hai đường thẳng song song thì:
* Cặp góc đồng vị bằng nhau
* Cặp góc so le trong bằng nhau.
* Cặp góc trong cùng phía bù nhau
Cách giải:
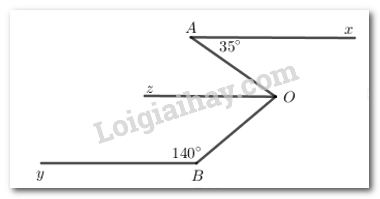
Kẻ \(Oz//Ax//By\)
Vì \(Ax//Oz\) nên \(\angle xAO = \angle zOA = 35^\circ \) (hai góc so le trong)
Vì \(Oz//By\) nên \(\angle yBO + \angle zOB = 180^\circ \) (hai góc trong cùng phía)
\(140^\circ + \angle zOB = 180^\circ \)
\( \Rightarrow \angle zOB = 180^\circ – 140^\circ = 40^\circ \)
Ta có: \(\angle AOB = \angle zOA + \angle zOB = 35^\circ + 40^\circ = 75^\circ \)
Bài 5
Hướng dẫn:
Để \(P = \frac{{M\left( x \right)}}{{n\left( x \right)}}\) có giá trị nguyên
+ Bước 1: Biến đổi \(P = m\left( x \right) + \frac{k}{{n\left( x \right)}}\). Trong đó \(k\) là số nguyên
+ Bước 2: Lập luận: Để \(P\) có giá trị nguyên thì \(k \vdots n\left( x \right)\) hay \(n\left( x \right) \in U\left( k \right)\)
+ Bước 3: Lập bảng giá trị và kiểm tra \(x\) với điều kiện đã tìm
+ Bước 4: Kết luận
Cách giải:
\(D = \frac{{\sqrt x + 2}}{{\sqrt x + 1}}\) (điều kiện: \(x \ge 0\))
\(\begin{array}{l} = \frac{{\sqrt x + 1 + 1}}{{\sqrt x + 1}}\\ = \frac{{\sqrt x + 1}}{{\sqrt x + 1}} + \frac{1}{{\sqrt x + 1}}\\ = 1 + \frac{1}{{\sqrt x + 1}}\end{array}\)
Để \(D \in \mathbb{Z}\) thì \(\frac{1}{{\sqrt x + 1}} \in \mathbb{Z}\)
Vì \(x \in \mathbb{Z}\) suy ra \(\sqrt x \in \mathbb{Z}\) (\(x\) là số chính phương) hoặc \(\sqrt x \in I\) (là số vô tỉ)
TH1: \(\sqrt x \) là số vô tỉ \( \Rightarrow \sqrt x + 1\) là số vô tỉ
\( \Rightarrow \frac{1}{{\sqrt x + 1}}\) là số vô tỉ (Loại)
TH2: \(\sqrt x \in \mathbb{Z} \Rightarrow \sqrt x + 1 \in \mathbb{Z}\)
\(\frac{1}{{\sqrt x + 1}} \in \mathbb{Z} \Rightarrow 1 \vdots \left( {\sqrt x + 1} \right)\) hay \(\left( {\sqrt x + 1} \right) \in \)Ư\(\left( 1 \right) = \left\{ { \pm 1} \right\}\)
Ta có bảng sau:
|
\(\sqrt x + 1\) |
\( – 1\) |
\(1\) |
|
\(\sqrt x \) |
\( – 2\) |
0 |
|
\(x\) |
Vô lí (vì \(\sqrt x = – 2\)) |
\(0\) ™ |
Vậy để \(D\) có giá trị nguyên thì \(x = 0\)