Giải và trình bày phương pháp giải Đề thi giữa kì 1 Toán 7 – Đề số 9 – Kết nối tri thức – Đề thi giữa kì 1 – Đề số 9 – Đề thi đề kiểm tra Toán lớp 7 Kết nối tri thức. Phần trắc nghiệm (3 điểm) Câu 1: Số đối của số hữu tỉ ( – 0,…
Đề thi:
Phần trắc nghiệm (3 điểm)
Câu 1: Số đối của số hữu tỉ \( – 0,25\) là
|
A. \( – 0,25.\) |
B. \(\frac{{ – 1}}{4}.\) |
|
C. \( – 4.\) |
D. \(0,25.\) |
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
|
A. \(\frac{0}{{ – 2}}\) |
B. \(\frac{{ – 2}}{{ – 1}}\) |
|
C. \( – \frac{1}{2}\) |
D. \(\frac{{ – \left( { – 2} \right)}}{3}\) |
Câu 3: Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
|
A. \(a < b.\) |
B. \(a > b.\) |
|
C. \(a = b.\) |
D. \(a = – b.\) |
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
|
A. \({7^9}.\) |
B. \({7^{11}}.\) |
|
C. \({7^{10}}.\) |
D. \({1^{10}}.\) |
Câu 5: Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a – b = c\) thì
|
A. \(a = b + c.\) |
B. \(a = – b + c.\) |
|
C. \(a = b – c.\) |
D. \(a = – b – c.\) |
Câu 6: Với \(x,y,z\) là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x – \left( {y + z} \right)\) bằng
|
A. \(x – y + z.\) |
B. \(x – y – z.\) |
|
C. \(x + y – z.\) |
D. \(x + y + z.\) |
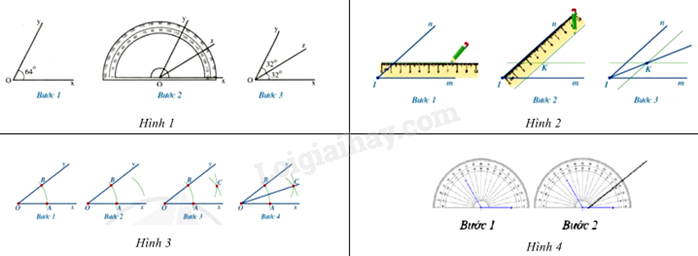
Câu 7: Trong các hình dưới đây, hình nào mô tả không đúng cách vẽ tia phân giác của một góc?
|
A. Hình 1. |
B. Hình 2. |
|
C. Hình 3. |
D. Hình 4. |
Sử dụng Hình 5 để trả lời các câu hỏi từ Câu 8 đến Câu 10.

Câu 8: Góc \({C_4}\) kề bù với góc nào?
|
A. Góc\({D_4}.\) |
B. Góc\({D_2}.\) |
|
C. Góc\({C_2}.\) |
D. Góc\({C_1}.\) |
Câu 9: Góc \({D_1}\) đối đỉnh với góc nào?
|
A. Góc\({D_1}\). |
B. Góc\({D_2}\). |
|
C. Góc \({D_3}\). |
D. Góc\({D_4}\). |
Câu 10: Nếu \(a{\rm{//}}b\) thì số đo góc \({D_1}\) bằng số đo
|
A. góc \({C_1}\). |
B. góc \({C_2}\). |
|
C. góc \({C_4}\). |
D. góc \({D_2}\). |
Câu 11: Qua một điểm nằm ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?
|
A. \(0.\) |
B. \(1.\) |
|
C. \(2.\) |
D. Vô số. |
Câu 12: Cho Hình 6, cần thêm điều kiện gì thì \(AB{\rm{//}}DC\)?

|
A. \(\widehat {BCD} = 60^\circ \) |
B. \(\widehat {BCD} = 120^\circ \) |
|
C. \(\widehat {BAD} = 60^\circ \) |
D. \(\widehat {xAB} = 60^\circ \) |
Phần tự luận (7 điểm)
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\)
Bài 2: (2,0 điểm) Thực hiện phép tính:
|
a) \(\left( { – 0,25} \right).40\; + 3\) |
b) \(\frac{1}{7} \cdot \frac{{ – 3}}{8} + \frac{{ – 13}}{8} \cdot \frac{1}{7}\) |
c) \(\left[ {\left( {\frac{2}{3} – \frac{1}{4}} \right) + {{\left( { – 2} \right)}^2}.3} \right] – 1\) |
Bài 3: (2,0 điểm) Tìm x, biết:
|
a) \(x – 4 = \frac{1}{2}\) |
b) \(2.\left( {x – 1} \right) = {3^3} – 1\) |
Bài 4: (1,5 điểm)
|
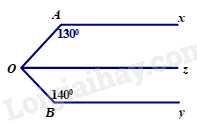
Cho Hình 7, biết \(Ax{\rm{//}}Oz\) và \(Ax{\rm{//}}By\). a) Tính số đo góc \(AOz.\) |
Hình 7 |
|
b) Chứng tỏ rằng góc \(AOB\) là góc vuông. |
|
|
c) Tia \(Oz\) có là tia phân giác của góc \(AOB\) không? Vì sao? |
Bài 5: (1,0 điểm)
Để nâng cao hiệu quả phòng chống dịch bệnh, học sinh phải thực hiện việc test nhanh Covid trước khi đến trường. Giá ban đầu để test mẫu gộp là \(40000\)đồng/1 học sinh, mẫu đơn là \(100000\)đồng/1 học sinh. Do lớp 7A test sau ngày 21/2/2022 nên được giảm giá 30%. Tính chi phí test nhanh Covid của lớp 7A biết có \(13\) em test mẫu gộp, \(22\) em test mẫu đơn.
——– Hết ——–
Đáp án Đề thi:
Phần trắc nghiệm (3 điểm)
|
Câu 1: D |
Câu 2: C |
Câu 3: B |
Câu 4: A |
Câu 5: A |
Câu 6: B |
|
Câu 7. D |
Câu 8. D |
Câu 9. C |
Câu 10. D |
Câu 11. B |
Câu 12. D |
Câu 1: Số đối của số hữu tỉ \( – 0,25\) là
|
A. \( – 0,25.\) |
B. \(\frac{{ – 1}}{4}.\) |
|
C. \( – 4.\) |
D. \(0,25.\) |
Hướng dẫn:
Số đối của một số hữu tỉ a là – a.
Lời giải
Số đối của -0,25 là -(-0,25) = 0,25.
Đáp án D.
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
|
A. \(\frac{0}{{ – 2}}\) |
B. \(\frac{{ – 2}}{{ – 1}}\) |
|
C. \( – \frac{1}{2}\) |
D. \(\frac{{ – \left( { – 2} \right)}}{3}\) |
Hướng dẫn:
Số hữu tỉ âm là số nhỏ hơn 0.
Lời giải
\(\frac{0}{{ – 2}} = 0\) nên không phải số hữu tỉ âm.
\(\frac{{ – 2}}{{ – 1}} = 2 > 0\) nên không phải số hữu tỉ âm.
\( – \frac{1}{2} < 0\) nên là số hữu tỉ âm.
\(\frac{{ – \left( { – 2} \right)}}{3} = \frac{2}{3} > 0\) nên không phải là số hữu tỉ âm.
Đáp án C.
Câu 3: Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
|
A. \(a < b.\) |
B. \(a > b.\) |
|
C. \(a = b.\) |
D. \(a = – b.\) |
Hướng dẫn:
Theo thứ tự trong tập hợp số hữu tỉ thì số nằm bên phải sẽ là số lớn hơn.
Lời giải
Vì điểm a nằm bên phải điểm b nên a > b.
Đáp án B.
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
|
A. \({7^9}.\) |
B. \({7^{11}}.\) |
|
C. \({7^{10}}.\) |
D. \({1^{10}}.\) |
Hướng dẫn:
Sử dụng quy tắc chia hai lũy thừa cùng cơ số.
Lời giải
\({7^{10}}:7 = {7^{10 – 1}} = {7^9}\).
Đáp án A.
Câu 5: Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a – b = c\) thì
|
A. \(a = b + c.\) |
B. \(a = – b + c.\) |
|
C. \(a = b – c.\) |
D. \(a = – b – c.\) |
Hướng dẫn:
Dựa vào quy tắc chuyển vế.
Lời giải
Nếu a – b = c thì a = b + c.
Đáp án A.
Câu 6: Với \(x,y,z\) là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x – \left( {y + z} \right)\) bằng
|
A. \(x – y + z.\) |
B. \(x – y – z.\) |
|
C. \(x + y – z.\) |
D. \(x + y + z.\) |
Hướng dẫn:
Dựa vào quy tắc dấu ngoặc.
Lời giải
Ta có: x – (y + z) = x – y – z.
Đáp án B.
Câu 7: Trong các hình dưới đây, hình nào mô tả không đúng cách vẽ tia phân giác của một góc?

|
A. Hình 1. |
B. Hình 2. |
|
C. Hình 3. |
D. Hình 4. |
Hướng dẫn:
Dựa vào cách vẽ tia phân giác đã học.
Lời giải
Trong các cách vẽ tia phân giác của một góc trên, chỉ có hình 4 chưa mô tả được đầy đủ cách để vẽ tia phân giác của một góc.
Đáp án D.
Sử dụng Hình 5 để trả lời các câu hỏi từ Câu 8 đến Câu 10.
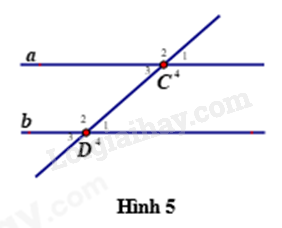
Câu 8: Góc \({C_4}\) kề bù với góc nào?
|
A. Góc \({D_4}.\) |
B. Góc \({D_2}.\) |
|
C. Góc \({C_2}.\) |
D. Góc \({C_1}.\) |
Hướng dẫn:
Hai góc kề bù là hai góc kề nhau và có tổng bằng 1800.
Lời giải
Quan sát hình vẽ, ta thấy góc \({C_4}\) kề bù với góc \({C_3}\) và góc \({C_1}\) nên ta chọn đáp án D.
Đáp án D.
Câu 9: Góc \({D_1}\) đối đỉnh với góc nào?
|
A. Góc \({D_1}\). |
B. Góc \({D_2}\). |
|
C. Góc \({D_3}\). |
D. Góc \({D_4}\). |
Hướng dẫn:
Dựa vào kiến thức hai góc đối đỉnh.
Lời giải
Quan sát hình vẽ, ta thấy góc \({D_1}\) đối đỉnh với góc \({D_3}\).
Đáp án C.
Câu 10: Nếu \(a{\rm{//}}b\) thì số đo góc \({D_1}\) bằng số đo
|
A. góc \({C_1}\). |
B. góc \({C_2}\). |
|
C. góc \({C_4}\). |
D. góc \({D_2}\). |
Hướng dẫn:
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Vì a // b nên \(\widehat {{C_1}} = \widehat {{D_1}}\)(hai góc đồng vị).
Đáp án A.
Câu 11: Qua một điểm nằm ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?
|
A. \(0.\) |
B. \(1.\) |
|
C. \(2.\) |
D. Vô số. |
Hướng dẫn:
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Đáp án B.
Câu 12: Cho Hình 6, cần thêm điều kiện gì thì \(AB{\rm{//}}DC\)?

|
A. \(\widehat {BCD} = 60^\circ \) |
B. \(\widehat {BCD} = 120^\circ \) |
|
C. \(\widehat {BAD} = 60^\circ \) |
D. \(\widehat {xAB} = 60^\circ \) |
Hướng dẫn:
Hai đường thẳng song song với nhau nếu hai góc đồng vị bằng nhau.
Lời giải
Để AB // DC thì \(\widehat {xAB} = \widehat {ADC}\) (hai góc đồng vị). Mà \(\widehat {ADC} = {60^0}\) nên để AB // DC thì \(\widehat {xAB} = 60^\circ \)
Đáp án D.
Phần tự luận.
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\).
Hướng dẫn:
Viết hai phân số về dạng số hữu tỉ để so sánh.
Lời giải
Ta có: \(0,25 = \frac{1}{4}\).
Vì 4 > 3 nên \(\frac{1}{4} < \frac{1}{3}\).
Vậy \(0,25 < \frac{1}{3}\).
Bài 2: (2,0 điểm) Thực hiện phép tính:
|
a) \(\left( { – 0,25} \right).40\; + 3\) |
b) \(\frac{1}{7} \cdot \frac{{ – 3}}{8} + \frac{{ – 13}}{8} \cdot \frac{1}{7}\) |
c) \(\left[ {\left( {\frac{2}{3} – \frac{1}{4}} \right) + {{\left( { – 2} \right)}^2}.3} \right] – 1\) |
Hướng dẫn:
Dựa vào quy tắc tính với số hữu tỉ để tính.
Lời giải
a) \(\left( { – 0,25} \right).40\; + 3\)
= -10 + 3
= -7
b) \(\frac{1}{7} \cdot \frac{{ – 3}}{8} + \frac{{ – 13}}{8} \cdot \frac{1}{7}\)
\(\begin{array}{l} = \frac{1}{7}\left( {\frac{{ – 3}}{8} + \frac{{ – 13}}{8}} \right)\\ = \frac{1}{7}\left( {\frac{{ – 3 – 13}}{8}} \right)\\ = \frac{1}{7}.\frac{{ – 16}}{8}\\ = \frac{1}{7}.\left( { – 2} \right)\\ = \frac{{ – 2}}{7}\end{array}\)
c) \(\left[ {\left( {\frac{2}{3} – \frac{1}{4}} \right) + {{\left( { – 2} \right)}^2}.3} \right] – 1\)
\( = {\rm{ }}\;\left[ {\frac{5}{{12}} + 12} \right] – 1\)
\( = {\rm{ }}\;\frac{{149}}{{12}} – 1\)
\( = {\rm{ }}\frac{{137}}{{12}}\)
Bài 3: (2,0 điểm) Tìm x, biết:
|
a) \(x – 4 = \frac{1}{2}\) |
b) \(2.\left( {x – 1} \right) = {3^3} – 1\) |
Hướng dẫn:
Sử dụng quy tắc chuyển vế để tìm x.
Lời giải
\({\rm{a) }}x – 4 = \frac{1}{2}\)
\({\rm{ }}x = \frac{1}{2} + 4\)
\({\rm{ }}x = \frac{9}{2}\)
Vậy \({\rm{ }}x = \frac{9}{2}\).
b) \(2.\left( {x – 1} \right) = {3^3} – 1\)
\(2.\left( {x – 1} \right) = 8\)
\(x – 1 = 4\)
\(\begin{array}{l}x = 4 + 1\\x = 5\end{array}\)
Vậy \(x = 5\).
Bài 4: (1,5 điểm)
|
Cho Hình 7, biết \(Ax{\rm{//}}Oz\) và \(Ax{\rm{//}}By\). a) Tính số đo góc \(AOz.\) |
Hình 7 |
|
b) Chứng tỏ rằng góc \(AOB\) là góc vuông. |
|
|
c) Tia \(Oz\) có là tia phân giác của góc \(AOB\) không? Vì sao? |
Hướng dẫn:
a) Góc xAO và góc AOz là hai góc trong cùng phía nên bù nhau.
b) Chứng minh \(\widehat {AOB} = \widehat {AOz} + \widehat {zOB} = {90^0}\).
c) Kiểm tra xem \(\widehat {{O_1}}\) và \(\widehat {{O_2}}\) có bằng nhau không.
Lời giải
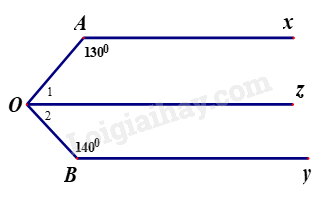
a) Vì \(Ax//Oz\) nên\(\widehat {AOz} + \widehat {OAx} = {180^0}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {AOz} = {180^0} – \widehat {OAx} = {180^0} – {130^0} = {50^0}\)
b) Vì \(Ax//Oz\)và \(Ax//By\) nên \(Oz//By\).
\( \Rightarrow \widehat {{O_2}} + \widehat {OBy} = {180^0}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{O_2}} = {180^0} – \widehat {OBy} = {180^0} – {140^0} = {40^0}\)
Do đó: \(\widehat {AOB} = \widehat {{O_1}} + \widehat {{O_2}} = {50^0} + {40^0} = {90^0}\).
Vậy AOB là góc vuông.
c) Tia Oz không là tia phân giác của góc \(AOB\) vì: \(\widehat {{O_1}} = {50^0} \ne {40^0} = \widehat {{O_2}}\).
Bài 5: (1,0 điểm)
Để nâng cao hiệu quả phòng chống dịch bệnh, học sinh phải thực hiện việc test nhanh Covid trước khi đến trường. Giá ban đầu để test mẫu gộp là \(40000\)đồng/1 học sinh, mẫu đơn là \(100000\)đồng/1 học sinh. Do lớp 7A test sau ngày 21/2/2022 nên được giảm giá 30%. Tính chi phí test nhanh Covid của lớp 7A biết có \(13\) em test mẫu gộp, \(22\) em test mẫu đơn.
Hướng dẫn:
Tính chi phí test Covid ban đầu.
Tính chi phí test Covid sau khi được giảm giá.
Lời giải
Chi phí test cô vít của lớp 7A khi chưa được giảm giá là:
\(13.40000 + 22.100000 = 2720000\)(đồng)
Chi phí test cô vít của lớp 7A sau khi được giảm giá là:
\(2720000.(100\% – 30\%) = 1904000\)(đồng)