Đáp án Lời giải Đề thi giữa kì 1 – Đề số 1 – Đề thi đề kiểm tra Toán lớp 7 Chân trời sáng tạo.
Câu hỏi/Đề bài:
I. TRẮC NGHIỆM ( 3 điểm)
|
Câu 1: D |
Câu 2: C |
Câu 3: D |
Câu 4: D |
Câu 5: B |
Câu 6: D |
Câu 1: Phân số biểu diễn số hữu tỉ -0,6 là:
A. \(\dfrac{6}{{10}}\) B. \(\dfrac{{ – 6}}{1}\) C. \(\dfrac{{ – 12}}{{10}}\) D. \(\dfrac{{18}}{{ – 30}}\)
Hướng dẫn:
Số thập phân \(\overline {0,a} = \dfrac{a}{{10}}\)
Lời giải
\( – 0,6 = \dfrac{{ – 6}}{{10}} = \dfrac{{( – 6).\left( { – 3} \right)}}{{10.\left( { – 3} \right)}} = \dfrac{{18}}{{ – 30}}\)
Chọn D
Câu 2: Kết quả của phép tính: \(\left( {\dfrac{2}{3} – \dfrac{5}{4}} \right):\dfrac{{21}}{{12}}\) là:
A. 3 B. -3 C. \(\dfrac{{ – 1}}{3}\) D. \(\dfrac{1}{3}\)
Hướng dẫn:
Tính biểu thức trong ngoặc trước rồi thực hiện phép chia.
Lời giải
\(\begin{array}{l}\left( {\dfrac{2}{3} – \dfrac{5}{4}} \right):\dfrac{{21}}{{12}} = \left( {\dfrac{8}{{12}} – \dfrac{{15}}{{12}}} \right).\dfrac{{12}}{{21}}\\ = \dfrac{{ – 7}}{{12}}.\dfrac{{12}}{{21}} = \dfrac{{ – 1}}{3}\end{array}\)
Chọn C
Câu 3: Giá trị của x trong biểu thức \( – {x^3} = 27\) là:
A. \( \pm 3\) B. \( \pm 9\) C. 3 D. -3
Hướng dẫn:
Đưa về dạng \({x^3} = {a^3} \Rightarrow x = a\)
Lời giải
\(\begin{array}{l} – {x^3} = 27\\{x^3} = – 27\\{x^3} = {\left( { – 3} \right)^3}\\x = – 3\end{array}\)
Vậy x = -3
Chọn D
Câu 4: Hình hộp chữ nhật có bao nhiêu cạnh?
- 4 B. 6 C. 8 D. 12
Hướng dẫn:
Hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh
Lời giải
Hình hộp chữ nhật có 12 cạnh.
Chọn D
Câu 5: Thể tích của hình lăng trụ đứng tứ giác có đáy là hình thoi có 2 đường chéo 8 cm, 12 cm; chiều cao 20 cm là:
A. \(960c{m^2}\) B. \(960c{m^3}\) C. \(192c{m^3}\) D. \(192c{m^2}\)
Hướng dẫn:
Thể tích hình lăng trụ đứng = Diện tích đáy. Chiều cao
Diện tích hình thoi = \(\dfrac{1}{2}\). Tích 2 đường chéo
Lời giải
Diện tích đáy của lăng trụ là: \(S = \dfrac{1}{2}.8.12 = 48\left( {c{m^2}} \right)\)
Thể tích hình lăng trụ đó là: \(V = S.h = 48.20 = 960\left( {c{m^3}} \right)\)
Chọn B
Câu 6: Để dán kín các mặt của hình lập phương cạnh 8 m cần diện tích giấy là bao nhiêu ?
- \(48{m^2}\) B. \(64{m^2}\)
C. \(512{m^2}\) D. \(384{m^2}\)
Hướng dẫn:
Diện tích toàn phần hình lập phương cạnh a là: Stp = 6 . a.a
Lời giải
Diện tích giấy dán là: Stp = 6 . a.a = 6. 8. 8 = 384 (m2)
Chọn D
II. TỰ LUẬN ( 7 ĐIỂM)
Câu 7: ( 1 điểm) Thực hiện phép tính (tính nhanh nếu có thể).
a) \(\dfrac{{13}}{{25}} – \dfrac{{31}}{{41}} + \dfrac{{12}}{{25}} – \dfrac{{10}}{{41}} – 0,5\)
b) \({( – 2)^3} – {\left( { – \dfrac{1}{2}} \right)^2}:\dfrac{{ – 1}}{{16}} – {2023^0}\)
Hướng dẫn:
Thứ tự thực hiện phép tính: Lũy thừa => Nhân, chia => Cộng, trừ
Sử dụng tính chất giao hoán của phép nhân, phép cộng
Lời giải
a)
\(\begin{array}{l}\dfrac{{13}}{{25}} – \dfrac{{31}}{{41}} + \dfrac{{12}}{{25}} – \dfrac{{10}}{{41}} – 0,5\\ = \left( {\dfrac{{13}}{{25}} + \dfrac{{12}}{{25}}} \right) + \left( { – \dfrac{{31}}{{41}} – \dfrac{{10}}{{41}}} \right) – 0,5\\ = \dfrac{{25}}{{25}} + \dfrac{{ – 41}}{{41}} – 0,5\\ = 1 + \left( { – 1} \right) – 0,5\\ = – 0,5\end{array}\)
b)
\(\begin{array}{l}{( – 2)^3} – {\left( { – \dfrac{1}{2}} \right)^2}:\dfrac{{ – 1}}{{16}} – {2023^0}\\ = \left( { – 8} \right) – \dfrac{1}{4}.\left( { – 16} \right) – 1\\ = \left( { – 8} \right) – \left( { – 4} \right) – 1\\ = \left( { – 8} \right) + 4 – 1\\ = – 5\end{array}\)
Câu 8: (1 điểm) Tìm x, biết:
a) \(\dfrac{1}{3}x – \dfrac{2}{5} = \dfrac{{ – 7}}{{15}}\) b) \({2^{x – 3}} – {3.2^x} + 92 = 0\)
Hướng dẫn:
a) Biến đổi để 1 vế là biểu thức chứa x, 1 vế chỉ chứa hệ số tự do.
b) Đưa về dạng \({a^x} = {a^b} \Rightarrow x = b\)
Lời giải
a)
\(\begin{array}{l}\dfrac{1}{3}x – \dfrac{2}{5} = \dfrac{{ – 7}}{{15}}\\\dfrac{1}{3}x = \dfrac{{ – 7}}{{15}} + \dfrac{2}{5}\\\dfrac{1}{3}x = \dfrac{{ – 7}}{{15}} + \dfrac{6}{{15}}\\\dfrac{1}{3}x = \dfrac{{ – 1}}{{15}}\\x = \dfrac{{ – 1}}{{15}}:\dfrac{1}{3}\\x = \dfrac{{ – 1}}{{15}}.3\\x = \dfrac{{ – 1}}{5}\end{array}\)
Vậy \(x = \dfrac{{ – 1}}{5}\)
b)
\(\begin{array}{l}{2^{x – 3}} – {3.2^x} + 92 = 0\\{2^{x – 3}} – {3.2^3}{.2^{x – 3}} = – 92\\{2^{x – 3}} – {24.2^{x – 3}} = – 92\\{2^{x – 3}}.\left( {1 – 24} \right) = – 92\\{2^{x – 3}}.\left( { – 23} \right) = – 92\\{2^{x – 3}} = \left( { – 92} \right):\left( { – 23} \right)\\{2^{x – 3}} = 4\\{2^{x – 3}} = {2^2}\\x – 3 = 2\\x = 5\end{array}\)
Vậy x = 5
Câu 9: (1 điểm)
Vào dịp Tết Nguyên đán, bà Ngọc dự định gói 20 cái bánh chưng cho gia đình. Nguyên liệu làm bánh gồm gạo nếp, đậu xanh, thịt lợn và lá dong. Mỗi cái bánh chưng sau khi gói nặng 0,75 kg gồm 0,45 kg gạo; 0,125 kg đậu xanh, 0,04 kg lá dong, còn lại là thịt. Hỏi khối lượng thịt bà cần chuẩn bị để gói bánh là khoảng bao nhiêu?
Hướng dẫn:
+ Tính khối lượng thịt trong 1 cái bánh chưng.
+ Tính khối lượng thịt trong 20 cái bánh chưng.
Lời giải
Khối lượng thịt trong 1 cái bánh chưng khoảng:
0,75 – (0,45 + 0,125 + 0,04) = 0,135 (kg)
Khối lượng thịt trong 20 cái bánh chưng khoảng:
0,135 . 20 = 2,7 (kg)
Vậy bà Ngọc cần chuẩn bị khoảng 2,7 kg thịt.
Câu 10: (3,5 điểm)
Hướng dẫn:
- a) Tính thể tích nước đổ vào.
Tính chiều rộng bể = Thể tích : (chiều cao . chiều dài)
b) Tính thể tích bể.
Tính chiều cao bể = Thể tích : ( chiều dài . chiều rộng)
2. a) Diện tích toàn phần = diện tích xung quanh + diện tích 2 đáy
Diện tích xung quanh lăng trụ đứng = chu vi đáy . chiều cao
Diện tích tam giác vuông = cạnh góc vuông . cạnh góc vuông : 2
b) Thể tích lăng trụ = Diện tích đáy . chiều cao
Lời giải
- a) Thể tích 120 thùng nước là: 120 . 20=2400 (l) = 2,4 m3
Chiều rộng của bể nước là: 2,4 : (3.0,8) = 1 (m)
b) Thể tích 60 thùng nước là: 60 . 20 = 1200 (l) = 1,2 m3
Do người ta đổ thêm 60 thùng nước nữa thì đầy bể, nên thể tích của bể là: V = 2,4 + 1,2 = 3,6 (m3)
Chiều cao của bể là: 3,6 : (3.1) = 1,2 (m)
2.
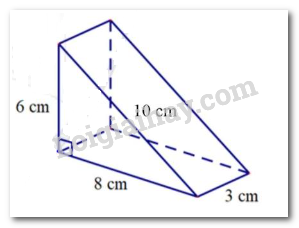
Bục có dạng hình lăng trụ tam giác có đáy là tam giác vuông có các cạnh lần lượt là 6cm, 8cm, 10cm; chiều cao là 3cm.
a) Diện tích xung quanh lăng trụ là: Sxq = (6+8+10) . 3 = 72 (cm2)
Diện tích đáy của lăng trụ là: Sđáy = 6.8:2=24 (cm2)
Diện tích cần sơn là: S = Sxq +2. Sđáy = 72 + 2.24 = 120 (cm2)
b) Thể tích lăng trụ là: V = Sđáy . h = 24 . 3 = 72 (cm3)
Câu 11: (0,5 điểm)
Tìm số hữu tỉ x sao cho:
\(\dfrac{{x + 1}}{{2023}} + \dfrac{{x + 2}}{{2022}} = \dfrac{{x + 3}}{{2021}} + \dfrac{{x + 4}}{{2020}}\)
Hướng dẫn:
Cộng cả 2 vế với 2
Lời giải
\(\begin{array}{l}\dfrac{{x + 1}}{{2023}} + \dfrac{{x + 2}}{{2022}} = \dfrac{{x + 3}}{{2021}} + \dfrac{{x + 4}}{{2020}}\\ \Leftrightarrow \left( {\dfrac{{x + 1}}{{2023}} + 1} \right) + \left( {\dfrac{{x + 2}}{{2022}} + 1} \right) = \left( {\dfrac{{x + 3}}{{2021}} + 1} \right) + \left( {\dfrac{{x + 4}}{{2020}} + 1} \right)\\ \Leftrightarrow \dfrac{{x + 2024}}{{2023}} + \dfrac{{x + 2024}}{{2022}} = \dfrac{{x + 2024}}{{2021}} + \dfrac{{x + 2024}}{{2020}}\\ \Leftrightarrow \dfrac{{x + 2024}}{{2023}} + \dfrac{{x + 2024}}{{2022}} – \dfrac{{x + 2024}}{{2021}} – \dfrac{{x + 2024}}{{2020}} = 0\\ \Leftrightarrow \left( {x + 2024} \right).\left( {\dfrac{1}{{2023}} + \dfrac{1}{{2022}} – \dfrac{1}{{2021}} – \dfrac{1}{{2020}}} \right) = 0\\ \Leftrightarrow \left( {x + 2024} \right) = 0\\ \Leftrightarrow x = – 2024\end{array}\)
Vậy x = -2024