Hướng dẫn cách giải/trả lời Đề thi giữa kì 1 Toán 7 – Đề số 8 – Cánh diều – Đề thi giữa kì 1 – Đề số 8 – Đề thi đề kiểm tra Toán lớp 7 Cánh diều. Phần trắc nghiệm (3 điểm) Câu 1. Chọn khẳng định đúng…
Đề thi:
Phần trắc nghiệm (3 điểm)
Câu 1. Chọn khẳng định đúng
|
A. \(\frac{3}{2} \in \mathbb{Q}.\) |
B. \(\frac{3}{2} \in \mathbb{Z}\). |
|
C. \(\frac{{ – 9}}{5} \notin \mathbb{Q}\). |
D. \( – 6 \in \mathbb{N}\). |
Câu 2. Số hữu tỉ dương là
|
A. \(\frac{{ – 11}}{3}.\) |
B. \( – \frac{{12}}{5}.\) |
|
C. \(\frac{{ – 5}}{{ – 7}}.\) |
D. \(\frac{{15}}{{ – 13}}.\) |
Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ – 21}}{{35}}\) là
|
A. \(\frac{3}{{35}}\). |
B. \(\frac{{ – 21}}{{35}}\). |
|
C. \(\frac{{ – 11}}{{35}}\). |
D. \(\frac{{11}}{{35}}\). |
Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} – x = \frac{1}{3}\) bằng
|
A. \(\frac{7}{{30}}.\) |
B. \(\frac{{ – 1}}{{15}}.\) |
|
C. \(\frac{{11}}{{15}}.\) |
D. \(\frac{1}{{15}}.\) |
Câu 5. Căn bậc hai số học của 81 là
|
A. 9 và -9 |
B. \(\frac{{ – 1}}{{81}}.\) |
|
C. \( – 9.\) |
D. \(9.\) |
Câu 6. Khẳng định đúng là
|
A. \(\left| { – 3,5} \right| = – 3,5\) |
B. \(\left| { – 3,5} \right| = 3,5.\) |
|
C. \(\left| { – 3,5} \right| = \pm 3,5\) |
D. \(\left| { – 3,5} \right| > 3,5.\) |
Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
|
A. \(\frac{{ – 7}}{{15}}\). |
B. \(\frac{{ – 7}}{{24}}\). |
|
C. \(\frac{{ – 5}}{{32}}\). |
D. \(\frac{{12}}{{45}}\). |
Câu 8. Giá trị của x trong đẳng thức – 0,6 = 1,4 là
|
A. 2 hoặc -2. |
B. 0,6 hoặc -0,6. |
|
C. 2. |
D. -2. |
Câu 9. Giá trị của đẳng thức\(\sqrt {2 + 3 + 4 + 3 + 4} \)
|
A. 16. |
B. -16. |
|
C. 4. |
D. -4. |
Câu 10. Những đồ vật sau có dạng hình gì?

|
A. Hình hộp chữ nhật |
B. Hình vuông |
|
C. Hình lập phương |
D. Hình chữ nhật |
Câu 11. Cho hình hộp chữ nhật có kích thước như hình vẽ.

Diện tích xung quanh của hình hộp chữ nhật là:
|
A. \(2750{\rm{c}}{{\rm{m}}^2}\) |
B. \(275{\rm{c}}{{\rm{m}}^2}\) |
|
C. \(2770{\rm{c}}{{\rm{m}}^2}\) |
D. \(27{\rm{c}}{{\rm{m}}^2}\) |
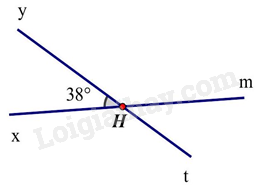
Câu 12. Cho hình bên dưới, biết số đo \(\widehat {xHy} = {38^0}\). Số đo \(\widehat {{\rm{yHm}}} = \) ?

|
A. \({38^0}\) |
B. \({142^0}\) |
|
C. \({52^0}\) |
D. \({128^0}\) |
PHẦN II. TỰ LUẬN (7 điểm)
Bài 1. ( 2,0 điểm)
1. So sánh: – 3,7634 và – 3,7654.
2. Thực hiện các phép tính sau
|
a. \(\frac{2}{9} – {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) |
b. \(17\frac{1}{3}.\left( {\frac{{ – 5}}{7}} \right) – 10\frac{1}{3}.\left( {\frac{{ – 5}}{7}} \right)\) |
Bài 2. ( 1,5 điểm) Tìm x, biết
|
a. x + 4,5 = 7,5 |
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\) |
c. |x| – 0,7 = 1,3 |
Bài 3. (2,5 điểm)
1. Cho một căn phòng có dạng hình hộp chữ nhật. Biết chiều dài, chiều rộng căn phòng lần lượt là 3m và 2m và chiều cao của căn phòng là 4m.a. Tính diện tích mặt sàn căn phòng.b. Để sơn xung quanh căn phòng cần trả bao nhiêu tiền công cho thợ sơn biết giá công sơn là 50 000 đồng cho mỗi m2 .
2. Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).

a. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\)
b. Kẻ đường thẳng c vuông góc với đường thẳng a tại M.
Chứng tỏ rằng: c \( \bot \) b
Bài 4. ( 1,0 điểm). So sánh A và B biết:
\(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\)
——– Hết ——–
Đáp án Đề thi:
Phần trắc nghiệm (3 điểm)
|
Câu 1: A |
Câu 2: C |
Câu 3: A |
Câu 4: D |
Câu 5: D |
Câu 6: B |
|
Câu 7. C |
Câu 8. A |
Câu 9. C |
Câu 10. C |
Câu 11. A |
Câu 12. B |
Câu 1. Chọn khẳng định đúng
|
A. \(\frac{3}{2} \in \mathbb{Q}.\) |
B. \(\frac{3}{2} \in \mathbb{Z}\). |
|
C. \(\frac{{ – 9}}{5} \notin \mathbb{Q}\). |
D. \( – 6 \in \mathbb{N}\). |
Hướng dẫn:
Dựa vào khái niệm các tập hợp đã học.
Lời giải
\(\frac{3}{2}\) là số hữu tỉ nên \(\frac{3}{2} \in \mathbb{Q}.\)
Đáp án A.
Câu 2. Số hữu tỉ dương là
|
A. \(\frac{{ – 11}}{3}.\) |
B. \( – \frac{{12}}{5}.\) |
|
C. \(\frac{{ – 5}}{{ – 7}}.\) |
D. \(\frac{{15}}{{ – 13}}.\) |
Hướng dẫn:
Dựa vào khái niệm số hữu tỉ.
Lời giải
\(\frac{{ – 5}}{{ – 7}} = \frac{5}{7}\) nên là số hữu tỉ dương.
Đáp án C.
Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ – 21}}{{35}}\) là
|
A. \(\frac{3}{{35}}\). |
B. \(\frac{{ – 21}}{{35}}\). |
|
C. \(\frac{{ – 11}}{{35}}\). |
D. \(\frac{{11}}{{35}}\). |
Hướng dẫn:
Dựa vào quy tắc tính với số hữu tỉ.
Lời giải
\(\begin{array}{l}\frac{3}{7} + \frac{4}{7}.\frac{{ – 21}}{{35}} = \frac{3}{7} + \frac{4}{7}.\frac{{ – 3}}{5} = \frac{3}{7} + \frac{{ – 12}}{{35}}\\ = \frac{{3.5 – 12}}{{35}} = \frac{3}{{35}}\end{array}\)
Đáp án A.
Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} – x = \frac{1}{3}\) bằng
|
A. \(\frac{7}{{30}}.\) |
B. \(\frac{{ – 1}}{{15}}.\) |
|
C. \(\frac{{11}}{{15}}.\) |
D. \(\frac{1}{{15}}.\) |
Hướng dẫn:
Sử dụng quy tắc trừ để tìm x.
Lời giải
\(\begin{array}{l}\frac{2}{5} – x = \frac{1}{3}\\x = \frac{2}{5} – \frac{1}{3}\\x = \frac{1}{{15}}\end{array}\).
Vậy \(x = \frac{1}{{15}}\)
Đáp án D.
Câu 5. Căn bậc hai số học của 81 là
|
A. 9 và -9. |
B. \(\frac{{ – 1}}{{81}}.\) |
|
C. \( – 9.\) |
D. \(9.\) |
Hướng dẫn:
Dựa vào kiến thức về căn bậc hai số học.
Lời giải
Căn bậc hai số học của 81 là 9.
Đáp án D.
Câu 6. Khẳng định đúng là
|
A. \(\left| { – 3,5} \right| = – 3,5\) |
B. \(\left| { – 3,5} \right| = 3,5.\) |
|
C. \(\left| { – 3,5} \right| = \pm 3,5\) |
D. \(\left| { – 3,5} \right| > 3,5.\) |
Hướng dẫn:
Dựa vào kiến thức về giá trị tuyệt đối.
Lời giải
Vì -3,5 < 0 nên |-3,5| = – (-3,5) = 3,5.
Đáp án B.
Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
|
A. \(\frac{{ – 7}}{{15}}\). |
B. \(\frac{{ – 7}}{{24}}\). |
|
C. \(\frac{{ – 5}}{{32}}\). |
D. \(\frac{{12}}{{45}}\). |
Hướng dẫn:
Dựa vào kiến thức về số thập phân hữu hạn.
Lời giải
\(\frac{{ – 7}}{{15}} = – 0,4(6)\).
\(\frac{{ – 7}}{{24}} = – 0,291(6)\).
\(\frac{{ – 5}}{{32}} = – 0,15625\).
\(\frac{{12}}{{45}} = 0,2(6)\).
Đáp án C.
Câu 8. Giá trị của x trong đẳng thức |x| – 0,6 = 1,4 là
|
A. 2 hoặc -2. |
B. 0,6 hoặc -0,6. |
|
C. 2. |
D. -2. |
Hướng dẫn:
Sử dụng quy tắc cộng và kiến thức về giá trị tuyệt đối để tìm x.
Lời giải
|x| – 0,6 = 1,4
|x| = 1,4 + 0,6
|x| = 2
Vậy x = 2 hoặc x = -2.
Đáp án A.
Câu 9. Giá trị của đẳng thức \(\sqrt {2 + 3 + 4 + 3 + 4} \)
|
A. 16. |
B. -16. |
|
C. 4. |
D. -4. |
Hướng dẫn:
Sử dụng quy tắc cộng và kiến thức về căn bậc hai để tính giá trị của đẳng thức.
Lời giải
\(\sqrt {2 + 3 + 4 + 3 + 4} = \sqrt {16} = 4\)
Đáp án C.
Câu 10. Những đồ vật sau có dạng hình gì?

|
A. Hình hộp chữ nhật |
B. Hình vuông |
|
C. Hình lập phương |
D. Hình chữ nhật |
Hướng dẫn:
Dựa vào đặc điểm của các hình đã học.
Lời giải
Các hình ảnh trên là hình lập phương.
Đáp án C.
Câu 11. Cho hình hộp chữ nhật có kích thước như hình vẽ.

Diện tích xung quanh của hình hộp chữ nhật là:
|
A. \(2750{\rm{c}}{{\rm{m}}^2}\) |
B. \(275{\rm{c}}{{\rm{m}}^2}\) |
|
C. \(2770{\rm{c}}{{\rm{m}}^2}\) |
D. \(27{\rm{c}}{{\rm{m}}^2}\) |
Hướng dẫn:
Dựa vào công thức tính diện tích xung quanh của hình hộp chữ nhật.
Lời giải
Đổi 2,5dm = 25cm.
Diện tích xung quanh của hình hộp chữ nhật là:
\({S_{xq}} = 2\left( {36 + 19} \right).25 = \)2750cm2.
Đáp án A.
Câu 12. Cho hình bên dưới, biết số đo \(\widehat {xHy} = {38^0}\). Số đo \(\widehat {{\rm{yHm}}} = \) ?
|
A. \({38^0}\) |
B. \({142^0}\) |
|
C. \({52^0}\) |
D. \({128^0}\) |
Hướng dẫn:
Dựa vào kiến thức về hai góc kề bù.
Lời giải
Ta có \(\widehat {xHy}\) và \(\widehat {yHm}\) là hai góc kề bù nên \(\widehat {xHy} + \widehat {yHm} = {180^0}\).
Suy ra \(\widehat {yHm} = {180^0} – \widehat {xHy} = {180^0} – {38^0} = {142^0}\).
Đáp án B.
Phần tự luận.
Bài 1. ( 2,0 điểm)
1. So sánh: – 3,7634 và – 3,7654.
2. Thực hiện các phép tính sau
|
a. \(\frac{2}{9} – {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) |
b. \(17\frac{1}{3}.\left( {\frac{{ – 5}}{7}} \right) – 10\frac{1}{3}.\left( {\frac{{ – 5}}{7}} \right)\) |
Hướng dẫn:
1. So sánh 3,7634 với 3,7654, số nào lớn hơn thì thêm dấu trừ sẽ là số nhỏ hơn.
2. Sử dụng các quy tắc tính toán với số hữu tỉ để thực hiện phép tính.
Lời giải
1. Ta có: 3,7634 – 3,7654.
2.
|
a. \(\frac{2}{9} – {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) \(\begin{array}{l} = \frac{2}{9} – \frac{1}{4} + \frac{5}{{18}}\\ = \left( {\frac{2}{9} + \frac{5}{{18}}} \right) – \frac{1}{4}\\ = \frac{1}{2} – \frac{1}{4}\\ = \frac{1}{4}\end{array}\) |
b. \(17\frac{1}{3}.\left( {\frac{{ – 5}}{7}} \right) – 10\frac{1}{3}.\left( {\frac{{ – 5}}{7}} \right)\) \(\begin{array}{l} = \left( {17\frac{1}{3} – 10\frac{1}{3}} \right).\left( {\frac{{ – 5}}{7}} \right)\\ = 7.\left( {\frac{{ – 5}}{7}} \right)\\ = – 5\end{array}\) |
Bài 2. ( 1,75 điểm) Tìm x, biết
|
a. x + 4,5 = 7,5 |
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\) |
c. |x| – 0,7 = 1,3 |
Hướng dẫn:
Dựa vào quy tắc tính để tìm x.
Lời giải
a. x + 4,5 = 7,5
x = 7,5 – 4,5
x = 3
Vậy x = 3.
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\)
\(\begin{array}{l}\frac{2}{3}.x = \frac{4}{9} – \frac{1}{2}\\\frac{2}{3}x = – \frac{1}{{18}}\\x = – \frac{1}{{18}}:\frac{2}{3}\\x = – \frac{1}{{12}}\end{array}\)
Vậy \(x = – \frac{1}{{12}}\).
c. |x| – 0,7 = 1,3
|x| = 1,3 + 0,7
|x| = 2
x = -2 hoặc x = 2.
Vậy x = -2 hoặc x = 2.
Bài 3. (2,25 điểm)
1. Cho một căn phòng có dạng hình hộp chữ nhật. Biết chiều dài, chiều rộng căn phòng lần lượt là 3m và 2m và chiều cao của căn phòng là 4m.a. Tính diện tích mặt sàn căn phòng.b. Để sơn xung quanh căn phòng cần trả bao nhiêu tiền công cho thợ sơn biết giá công sơn là 50 000 đồng cho mỗi m2 .
2. Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).
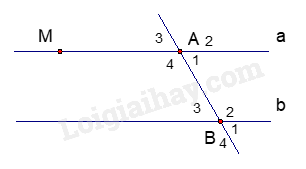
a. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\)
b. Kẻ đường thẳng c vuông góc với đường thẳng a tại M.
Chứng tỏ rằng: c \( \bot \) b
Hướng dẫn:
1.
a. Dựa vào công thức tính diện tích hình chữ nhật.
b. Tính diện tích xung quanh căn phòng.
Số tiền công = diện tích xung quanh . giá công sơn.
2.
a. Dựa vào hai góc đối đỉnh và tính chất các góc của hai đường thẳng song song.
b. Dựa vào quan hệ giữa tính vuông góc và song song.
Lời giải
1.

a. Diện tích mặt sàn là: 3.2 = 6 (m )2.b. Diện tích cần sơn của căn phòng là: 2.4.(3 + 2) = 40 (m )2.Để sơn xung quanh căn phòng cần trả số tiền công cho thợ sơn là:50 000.40 = 2 000 000 (đồng)Vậy để sơn xung quanh căn phòng cần trả 2 000 000 đồng cho thợ sơn.
2.

a. Ta có \(\widehat {{A_1}}\) và \(\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}}\) = \(\widehat {{A_3}}\) = 700.
Vì a // b nên ta có \(\widehat {{A_3}} = \widehat {{B_3}}\) (hai góc đồng vị) nên \(\widehat {{A_3}}\)= \(\widehat {{B_3}}\) = 700.
b. Vì a \( \bot \) c và a // b nên b \( \bot \) c (mối quan hệ giữa tính vuông góc và song song.
Bài 4. ( 1,0 điểm). So sánh A và B biết:
\(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\)
Hướng dẫn:
Nhân cả A và B với 2023, đưa A và B về so sánh 2 phân số cùng tử, từ đó so sánh được A và B.
Lời giải
Nhân A với 2023, ta được: \(2023A = \frac{{2023\left( {{{2023}^{2023}} + 1} \right)}}{{{{2023}^{2024}} + 1}} = \frac{{{{2023}^{2024}} + 2023}}{{{{2023}^{2024}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}}\).
Nhân B với 2023, ta được: \(2023B = \frac{{2023\left( {{{2023}^{2022}} + 1} \right)}}{{{{2023}^{2023}} + 1}} = \frac{{{{2023}^{2023}} + 2023}}{{{{2023}^{2023}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\).
Ta có:
\(\begin{array}{l}{2023^{2024}} > {2023^{2023}}\\{2023^{2024}} + 1 > {2023^{2023}} + 1\\\frac{1}{{{{2023}^{2024}} + 1}} < \frac{1}{{{{2023}^{2023}} + 1}}\\\frac{{2022}}{{{{2023}^{2024}} + 1}} < \frac{{2022}}{{{{2023}^{2023}} + 1}}\\1 + \frac{{2022}}{{{{2023}^{2024}} + 1}} < 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\\2023A < 2023B\\A < B\end{array}\)
Vậy A < B.