Giải chi tiết Bài tập (Chủ đề 4) trang 53 Khoa học tự nhiên 7 Cánh diều – Chủ đề 4. Tốc độ – sách Khoa học tự nhiên 7 Cánh diều. Một chiếc xe đi được quãng đường 600m trong 30s. Tốc độ của xe là bao nhiêu….
| Câu 1: Một chiếc xe đi được quãng đường 600m trong 30s. Tốc độ của xe là bao nhiêu? |
Hướng dẫn:
– Xác định tốc độ chuyển động của xe theo công thức: \(\)\(v = \frac{s}{t}\)
Lời giải:
Tốc độ chuyển động của xe là: \(v = \frac{s}{t} = \frac{{600}}{{30}} = 20(m/s)\)
|
Câu 2: Một chiếc xe đang đi với tốc độ 8m/s. – Xe đi được bao xa trong 8s? – Cần bao lâu để xe đi được 160m? |
Hướng dẫn:
– Tốc độ chuyển động của xe tính theo công thức: \(\)\(v = \frac{s}{t} \Rightarrow \left\{ \begin{array}{l}s = v.t\\t = \frac{s}{v}\end{array} \right.\)
Lời giải:
– Quãng đường xe đi được trong 8s là: s = v.t = 8.8 = 64 (m/s)
– Thời gian để đi được 160m là: \(t = \frac{s}{v} = \frac{{160}}{8} = 20(s)\)
|
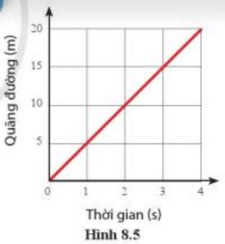
Câu 3: Tính tốc độ chuyển động dựa vào đồ thị quãng đường – thời gian của chuyển động H 8.5.
|
Hướng dẫn:
– Với mỗi đoạn đồ thị để xác định thời gian chuyển động ta làm như sau:
+ Từ điểm đầu, kẻ đường thẳng vuông góc với trục thời gian, để xác định thời điểm bắt đầu tính chuyển động: t1
+ Từ điểm cuối, kẻ đường thẳng vuông góc với trục thời gian, để xác định thời điểm cuối tính chuyển động: t2
=> Thời gian chuyển động, là hiệu 2 thời gian trên: t = t2 – t1
– Với mỗi đoạn đồ thị để xác định quãng đường chuyển động ta làm như sau:
+ Từ điểm đầu, kẻ đường thẳng vuông góc với trục quãng đường, để xác định vị trí bắt đầu tính chuyển động: s1
+ Từ điểm cuối, kẻ đường thẳng vuông góc với trục quãng đường, để xác định vị trí cuối tính chuyển động: s2
=> Quãng đường chuyển động là hiệu hai vị trí trên: s = s2 – s1
– Xác định tốc độ chuyển động của mỗi xe theo công thức: \(\)\(v = \frac{s}{t}\)
Lời giải:
– Từ đồ thị ta thấy:
+ Thời gian chuyển động của xe là t = 4s
+ Quãng đường xe đã đi là: s = 20m
– Vậy, tốc độ chuyển động của xe là: \(\)\(v = \frac{s}{t} = \frac{{20}}{4} = 5(m/s)\)
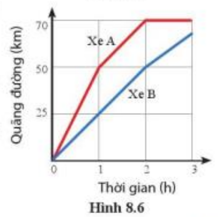
| Câu 4: Trong hình 8.6, đường màu đỏ và đường màu xanh lần lượt biểu diễn đồ thị quãng đường – thời gian của xe A và xe B trong một chuyến đi dài. |
| a) Tính quãng đường xe A đi được trong một giờ đầu? |
Hướng dẫn:
– Với mỗi đoạn đồ thị để xác định quãng đường chuyển động ta làm như sau:
+ Từ điểm đầu, kẻ đường thẳng vuông góc với trục quãng đường, để xác định vị trí bắt đầu tính chuyển động: s1
+ Từ điểm cuôi, kẻ đường thẳng vuông góc với trục quãng đường, để xác định vị trí cuối tính chuyển động: s2
=> Quãng đường chuyển động là hiệu hai vị trí trên: s = s2 – s1
Lời giải chi tiết:
Từ đồ thị ta thấy: Trong 1 giờ đầu xe A đi được quãng đường là 50km.
| b) Tốc độ của xe A thay đổi như thế nào trong giờ thứ 2 của chuyến đi? |
Hướng dẫn:
Với mỗi đoạn đồ thị để xác định thời gian chuyển động ta làm như sau:
+ Từ điểm đầu, kẻ đường thẳng vuông góc với trục thời gian, để xác định thời điểm bắt đầu tính chuyển động: t1
+ Từ điểm cuôi, kẻ đường thẳng vuông góc với trục thời gian, để xác định thời điểm cuối tính chuyển động: t2
=> Thời gian chuyển động, là hiệu 2 thời gian trên: t = t2 – t1
– Xác định tốc độ chuyển động của mỗi xe theo công thức: \(\)\(v = \frac{s}{t}\)
– Xe nào có tốc độ lớn hơn sẽ chuyển động nhanh hơn.
Lời giải:
Trong giờ thứ 2 của chuyện động, đồ thị của xe A có hướng đi lên, chứng tỏ tốc độ của xe A đang tăng.
| c) Xe B chuyển động nhanh hơn hay chậm hơn xe A trong một giờ đầu tiên? |
Lời giải:
Tốc độ của xe A trong 1 giờ đầu là: \(v = \frac{s}{t} = \frac{{50}}{1} = 50(km/h)\)
Tốc độ của xe B trong 1 giờ đầu là: \(v = \frac{s}{t} = \frac{{25}}{1} = 25(km/h)\)
Vì vA > vB, nên trong một giờ đầu xe B chuyển động chậm hơn xe A.