Tìm chiều cao của hình bình hành CBEG: \(h = \frac{S}{a}\) với a là độ dài cạnh BE, S là diện tích. Gợi ý giải Giải bài 2 trang 104 SGK Toán 6 Cánh diều – Bài 3. Hình bình hành. Một mảnh đất có dạng hình bình hành ABCD với AB = 47 m….
Đề bài/câu hỏi:
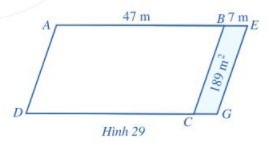
Một mảnh đất có dạng hình bình hành ABCD với AB = 47 m. Người ta mở rộng mảnh đất này thành hình bình hành AEGD có diện tích lớn hơn diện tích mảnh đất ban đầu là 189 \({m^2}\) và BE = 7m ( Hình 29). Tính diện tích mảnh đất ban đầu.
Hướng dẫn:
– Tìm chiều cao của hình bình hành CBEG: \(h = \frac{S}{a}\) với a là độ dài cạnh BE, S là diện tích.
– Chiều cao của hình bình hành CBEG bằng chiều cao của hình bình hành ABCD.
Lời giải:
Chiều cao ứng với đáy BE của hình bình hành CBEG là: 189 : 7 = 27 m.
Chiều cao ứng với đáy AB của hình bình hành ABCD cũng là: 27 m.
Diện tích mảnh đất ABCD ban đầu là: 47 x 27 = 1269 (\({m^2}\))