Đáp án Đề bài Đề thi học kì 2 – Đề số 1 – Đề thi đề kiểm tra Toán lớp 6 Kết nối tri thức.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 Một người đi xe máy đoạn đường AB với vận tốc \(26\dfrac{1}{4}\) km/h hết \(2,4\) giờ. Lúc về, người ấy đi với vận tốc \(30\) km/h. Tính thời gian người ấy đi từ B đến A?
A. \(2\) giờ \(5\) phút B. \(2\) giờ \(6\) phút C. \(2\) giờ D. \(2\) giờ \(4\) phút
Câu 2 Góc bẹt có số đo bằng:
A. \({180^0}\) B. \({90^0}\) C. \({60^0}\) D. \({0^0}\)
Câu 3 Gieo một con xúc xắc \(4\) mặt \(50\) lần và quan sát số ghi trên đỉnh của con xúc xắc, ta được kết quả như sau:
Tính xác suất thực nghiệm để gieo được đỉnh có số chẵn:
A. \(\dfrac{9}{{50}}\) B. \(\dfrac{{14}}{{50}}\) C. \(\dfrac{{15}}{{50}}\) D. \(\dfrac{{23}}{{50}}\)
Câu 4
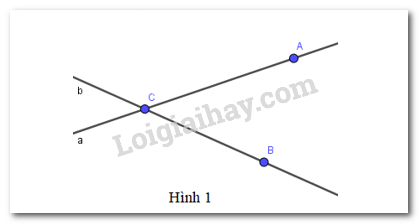
Chọn phát biểu sai trong các phát biểu sau:
A. Điểm A thuộc đường thẳng a
B. Hai điểm A, B cùng thuộc đường thẳng a
C. Điểm C thuộc đường thẳng b
D. Hai điểm B, C cùng thuộc đường thẳng b
Phần II. Tự luận (8 điểm):
Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể):
a) \({\kern 1pt} \dfrac{1}{5} + \dfrac{{ – 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ – 4}}{{19}}\) b) \({\kern 1pt} \dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\)
c) \({\kern 1pt} 25\% {\rm{\;}} – 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}\) d) \({\kern 1pt} {\left( {\dfrac{{ – 1}}{6}} \right)^2}:\dfrac{5}{{ – 24}} + \left( {\dfrac{7}{{25}} – 36\% } \right).\left| { – 8\dfrac{1}{3}} \right|\)
Bài 2: (1,5 điểm) Tìm x, biết:
Tìm \(x\), biết:
a) \({\kern 1pt} x:\dfrac{2}{5} = \dfrac{{ – 15}}{4}\) b) \({\kern 1pt} \dfrac{2}{3}.x – \dfrac{1}{2} = 1\dfrac{1}{2}\) c) \({\kern 1pt} 0,6.x + 40\% x = 9\)
Bài 3: (1,5 điểm) Có một tập bài kiểm tra gồm 45 bài được xếp thành ba loại: Giỏi, khá và trung bình. Trong đó số bài đạt điểm giỏi bằng \(\dfrac{1}{3}\) tổng số bài kiểm tra. Số bài đạt điểm khá bằng \(90\% \) số bài còn lại.
a) Tính số bài trung bình.
b) Tính tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra.
Bài 4: (2,5 điểm) Cho hai điểm \(M,N\) thuộc tia \(Ox\) sao cho \(OM = 2cm;ON = 5cm\). Điểm \(P\) thuộc tia đối của tia \(Ox\) sao cho \(OP = 3cm\).
a) Điểm \(M\) có nằm giữa hai điểm \(O\) và \(N\) không? Tại sao? Tính \(MN.\)
b) So sánh\(MN\) và \(OP.\)
c) Gọi \(I\) là trung điểm của \(OM\). Tính \(IO\) và \(IP.\)
d) Điểm \(I\) có là trung điểm của \(NP\) không? Tại sao?
Bài 5: (0,5 điểm) Cho \(S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + … + \dfrac{5}{{{{100}^2}}}\)
Chứng minh rằng \(2 < S < 5\)