Giải chi tiết Lời giải Đề thi giữa kì 1 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 6 Chân trời sáng tạo.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm
|
1. A |
2. C |
3. C |
4. B |
5. D |
6. B |
|
7. C |
8. B |
9. A |
10. C |
11. B |
12. B |
Câu 1
Hướng dẫn:
Vận dụng kiến thức về tập hợp số tự nhiên khác \(0\)
Cách giải:
Tập hợp số tự nhiên \({\mathbb{N}^*}\) là \({\mathbb{N}^*} = \left\{ {1;2;3;…} \right\}\)
Chọn A.
Câu 2
Hướng dẫn:
Vận dụng kiến thức về tập hợp, phần tử của tập hợp.
Hai cách viết tập hợp:
– Cách 1: Liệt kê các phần tử có trong tập hợp.
– Cách 2: Mô tả đặc trưng của các phần tử có trong tập hợp.
Cách giải:
Tập hợp \(A\) gồm các số tự nhiên lớn hơn \(0\) và nhỏ hơn \(6\) nên ta cách viết \(A = \left\{ {x \in \mathbb{N}\left| {x < 6} \right.} \right\}\) là sai vì phần tử \(0 \notin A\)
Chọn C.
Câu 3
Hướng dẫn:
Vận dụng quy tắc nhân lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
Cách giải:
Ta có: \({6^5}{.6^3} = {6^{5 + 3}} = {6^8}\)
Chọn C.
Câu 4
Hướng dẫn:
Vận dụng kiến thức về lũy thừa bậc \(n\) của \(a\) để tính giá trị
Cách giải:
Ta có: \({10^8} = 10.10.10.10.10.10.10.10 = 100000000\)
Chọn B.
Câu 5
Hướng dẫn:
Vận dụng quy tắc nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
Vận dụng quy tắc chia hai lũy thừa cùng cơ số (khác \(0\)), ta giữ nguyên cơ số và trừ các số mũ.
Cách giải:
Ta có: \({a^m}.{a^n} = {a^{m + n}}\)
Chọn D.
Câu 6
Hướng dẫn:
Thực hiện phép chia để xác định thương và số dư của phép chia
Cách giải:
Đáp án A sai vì: Phép chia \(1584\) cho \(132\) có thương là \(12\) và có số dư là \(0\)
Đáp án B đúng vì: Phép chia \(1983\) chia cho \(15\) có thương là \(132\) và có số dư là \(3\)
Đáp án C sai vì: Phép chia \(9755\) cho \(75\) có thương là \(130\) và có số dư là \(5\)
Đáp án D sai vì: Phép chia \(485\) chia cho \(32\) có thương là \(15\) và có số dư \(5\)
Chọn B.
Câu 7
Hướng dẫn:
Vận dụng dấu hiệu chia hết cho\(2\) và dấu hiệu chia hết cho \(5\) để đưa ra kết luận.
Cách giải:
Số có chữ số tận cùng là \(0;2;4;6;8\) thì chia hết cho \(2\).
Số có chữ số tận cùng là \(0;5\) thì chia hết cho \(5\).
Vậy số có chữ số tận cùng là \(0\) thì chia hết cho cả \(2\) và \(5\).
Chọn C.
Câu 8
Hướng dẫn:
Phân tích một số ra thừa số nguyên tố theo cột dọc
Cách giải:
\(\left. \begin{array}{l}270\\135\\45\\15\\5\\1\end{array} \right|\begin{array}{*{20}{c}}2\\\begin{array}{l}3\\3\\3\\5\\\end{array}\end{array}\)
Vậy \(270 = {2.3^3}.5\)
Chọn B.
Câu 9
Hướng dẫn:
Vận dụng kiến thức về hợp số là gì? Hợp số là số tự nhiên lớn hơn \(1\) có nhiều hơn hai ước.
Cách giải:
Ta có: \(34 > 1\) và Ư\(\left( {34} \right) = \left\{ {1;2;17} \right\}\)
Chọn A.
Câu 10
Hướng dẫn:
Vận dụng đặc điểm hình học của hình vuông.
Cách giải:
Trong hình vuông: Bốn góc vuông và bốn cạnh bằng nhau.
Chọn C.
Câu 11
Hướng dẫn:
Tính chiều rộng của hình chữ nhật
Áp dụng công thức tính diện tích hình chữ nhật
Cách giải:
Chiều rộng hình chữ nhật là: \(12:2 = 6\left( {cm} \right)\)
Diện tích hình chữ nhật là: \(12.6 = 72\left( {c{m^2}} \right)\)
Chọn B.
Câu 12
Hướng dẫn:
Nhận biết được công thức tính diện tích hình thoi
Cách giải:
\(S = \dfrac{{AC.BD}}{2}\)
Chọn B.
Phần II: Tự luận
Bài 1
Hướng dẫn:
Liệt kê các phần tử có trong tập hợp.
Cách giải:
a) \(A = \left\{ {1;2;3;4;5;6;7} \right\}\)
b)
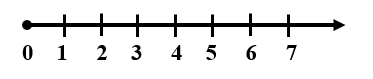
Bài 2
Hướng dẫn:
Vận dụng các phép tính cộng, trừ, nhân, chia các số tự nhiên; phép nâng lên lũy thừa, thứ tự thực hiện phép tính, tính chất phân phối của phép nhân đối với phép cộng (trừ).
Cách giải:
|
a) \({5^3}.4 – \left( {{1^0} + 24} \right):{5^2}\) \(\begin{array}{l} = 125.4 – \left( {1 + 24} \right):25\\ = 500 – 25:25\\ = 500 – 1\\ = 499\end{array}\) |
b) \(13.85 + 87.85 – 500\) \(\begin{array}{l} = 85.\left( {13 + 87} \right) – 500\\ = 85.100 – 500\\ = 8500 – 500\\ = 8000\end{array}\) |
Bài 3
Hướng dẫn:
Giải bài toán ngược để tìm \(x\).
Cách giải:
|
a) \(84 – 9.\left( {3x + 1} \right) = 48\) \(\begin{array}{l}9.\left( {3x + 1} \right) = 84 – 48\\9.\left( {3x + 1} \right) = 36\\3x + 1 = 36:9\\3x + 1 = 4\\3x = 3\\x = 1\end{array}\) Vậy \(x = 1\) |
b) \(\left[ {\left( {4x – 24} \right):5} \right].64 = 1024\) \(\begin{array}{l}\left( {4x – 24} \right):5 = 16\\4x – 24 = 16.5\\4x – 24 = 80\\4x = 104\\x = 104:4\\x = 26\end{array}\) Vậy \(x = 26\) |
Bài 4
Hướng dẫn:
1. a) Vận dụng các bước vẽ hình tam giác đều.
b) Vận dụng các bước vẽ hình chữ nhật.
2. Chu vi hình thoi cạnh a là: C = 4.a
Cách giải:
1. a) – Bước 1: Vẽ đoạn thẳng \(AB = 5cm\)
– Bước 2: Lấy \(A;B\) làm tâm, vẽ hai đường tròn bán kính \(5cm\).
– Bước 3: Gọi \(C\) là một trong hai giao điểm của hai đường tròn. Nối \(C\) với \(A\) và nối \(C\) với \(B\) ta được tam giác \(ABC\).
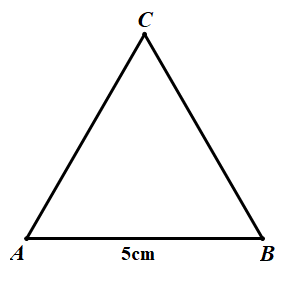
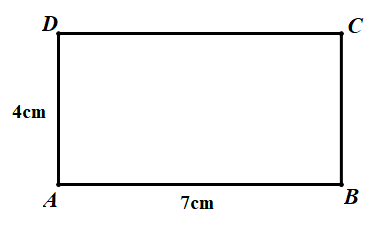
b) – Bước 1: Vẽ đoạn thẳng \(AB = 7cm\) và \(AD = 4cm\) vuông góc với nhau.
– Bước 2: Qua \(B\) vẽ đường thẳng vuông góc với \(AB\).
– Bước 3: Qua \(D\) vẽ đường thẳng vuông góc với \(AD\).
Hai đường thẳng này cắt nhau ở \(C\). Khi đó, ta được \(ABCD\) là hình chữ nhật cần vẽ.
2. Độ dài cạnh của hình thoi có chu vi 64 dm là:
64 : 4 = 16 (dm)
Bài 5
Hướng dẫn:
Gọi số học sinh của khối 9 là \(x\) (\(x \in {\mathbb{N}^*};200 \le x \le 250\))
Tìm BCNN\(\left( {10,12,15} \right)\), từ đó xác định BC\(\left( {10,12,15} \right)\)( là bội của BCNN)
Đối chiếu điều kiện, kết luận.
Cách giải:
Gọi số học sinh của khối 9 là \(x\) với \(x \in {\mathbb{N}^*};200 \le x \le 250\)
Vì số học sinh của khối \(9\) chia cho \(10\) học sinh, \(12\) học sinh hay \(15\) học sinh thì đều không thừa học sinh nào nên: \(x \vdots 10;x \vdots 12;x \vdots 15\)
Suy ra, \(x \in \)BC\(\left( {10,12,15} \right)\)
Ta có: \(10 = 2.5\); \(12 = {2^2}.3\); \(15 = 3.5\)
Suy ra, BCNN\(\left( {10,12,15} \right) = {2^2}.3.5 = 60\)
Nến BC\(\left( {10,12,15} \right) = \left\{ {0;60;120;180;240;300;…} \right\}\)
Mà \(200 \le x \le 250\), suy ra \(x = 240\)
Vậy khối \(9\)của trường có \(240\) học sinh.
Bài 6
Hướng dẫn:
Vận dụng công thức tính diện tích hình thang
Tính chi phí cần mua cỏ để trải \(1d{m^2}\)
Tính chi phi cần mua cỏ để trải kín sân vườn
Cách giải:
Diện tích của mảnh vườn là:
\(\dfrac{{\left( {24 + 68} \right).32}}{2} = 1472\left( {d{m^2}} \right)\)
Chi phí cần mua cỏ để trải \(1d{m^2}\) là:
\(120000:8 = 15000\) (đồng)
Chi phí cần mua cỏ để trải kín sân vườn là:
\(15000.1472 = 22080000\) (đồng)