Trả lời Lời giải Đề thi giữa kì 1 – Đề số 3 – Đề thi đề kiểm tra Toán lớp 6 Chân trời sáng tạo.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm
|
1. A |
2. D |
3. C |
4. D |
5. D |
6. B |
|
7. D |
8. A |
9. D |
10. A |
11. C |
12. C |
Câu 1
Hướng dẫn:
Vận dụng cách viết tập hợp bằng cách liệt kê các phần tử:
– Tên của tập hợp thường được kí hiệu là chữ cái in hoa
– Các phần tử của tập hợp được đặt trong dấu ngoặc nhọn và cách nhau bởi dấu chấm phẩy: “;”
– Các phần tử trong tập hợp được liệt kê duy nhất 1 lần, theo thứ tự tùy ý.
Cách giải:
Cách viết \(A = \left\{ {9;3;5;1} \right\}\) là đúng.
Chọn A.
Câu 2
Hướng dẫn:
Vận dụng cách viết tập hợp bằng cách liệt kê các phần tử:
– Tên của tập hợp thường được kí hiệu là chữ cái in hoa
– Các phần tử của tập hợp được đặt trong dấu ngoặc nhọn và cách nhau bởi dấu chấm phẩy: “;”
– Các phần tử trong tập hợp được liệt kê duy nhất 1 lần, theo thứ tự tùy ý.
Cách giải:
Đáp án A. \(\left\{ {QUANG;NGAI} \right\}\) sai vì đây là tập hợp các từ có trong cụm từ QUẢNG NGÃI.
Đáp án B. \(\left\{ {Q;U;A;N;G;N;G;A;I} \right\}\) sai vì trong tập hợp này có phần tử là chữ cái A; N; G bị lặp lại hai lần.
Đáp án C. \(\left\{ {Q;U;A;N;G;A;I} \right\}\) sai vì trong tập hợp này có phần tử là chữ cái A bị lặp lại hai lần.
Đáp án D. \(\left\{ {Q;U;A;N;G;I} \right\}\) đúng.
Chọn D.
Câu 3
Hướng dẫn:
Xác định giá trị của chữ số \(2\) và giá trị của chữ số \(4\)của số \(19254\)
Thực hiện phép chia để xác định mối quan hệ giữa giá trị của chữ số \(2\) và giá trị của chữ số \(4\)
Cách giải:
Giá trị của chữ số \(2\) của số \(19254\) là \(200\)
Giá trị của chữ số \(4\)của số \(19254\) là \(4\)
Ta có: \(200:4 = 50\)
Vậy giá trị của chữ số \(2\) bằng \(50\) lần giá trị của chữ số \(4\).
Chọn C.
Câu 4
Hướng dẫn:
Định nghĩa lũy thừa của một số tự nhiên: \(a.a \ldots .a{\rm{ }} = {a^n}\) ( n thừa số a)
Cách giải:
Ta có: \(5.5.5.5 = {5^4}\)
Chọn D.
Câu 5
Hướng dẫn:
Vận dụng cách ghi số tự nhiên trong hệ thập phân.
Cách giải:
Ta có: \(a = 48053 = 40000 + 8000 + 50 + 3\)
Chọn D.
Câu 6
Hướng dẫn:
Áp dụng tính chất chia hết của một tổng: “Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó”.
Cách giải:
Nếu \(a \vdots 3\) và \(b \vdots 3\) thì \(\left( {a + b} \right) \vdots 3\)
Vậy … là \(\left( {a + b} \right) \vdots 3\).
Chọn B.
Câu 7
Hướng dẫn:
Vận dụng dấu hiệu chia hết cho \(2;3;5\) và \(9\).
Cách giải:
Số chia hết cho \(2\) và \(5\) có chữ số tận cùng là \(0\) nên loại đáp án C
Số chia hết cho \(3\) có tổng các chữ số chia hết cho \(3\) nên loại đáp án B
Số chia hết cho \(9\) có tổng các chữ số chia hết cho \(9\) nên loại đáp án A
Vậy số chia hết cho \(2;3;5\) và \(9\) trong bốn đáp án là \(900\)
Chọn D.
Câu 8
Hướng dẫn:
Nhân lượt lượt \(9\) với \(0;1;2;3;…\) ta xác định được các bội của \(9\).
Cách giải:
Ta có: \(504 = 9.56\)
Chọn B.
Câu 9
Hướng dẫn:
Vận dụng định nghĩa số nguyên tố là số tự nhiên lớn hơn \(1\), chỉ có hai ước là \(1\) và chính nó.
Cách giải:
\(13k\) là số nguyên tố nên \(k = 1\)
Chọn D.
Câu 10
Hướng dẫn:
Vận dụng các đặc điểm của hình thoi, hình chữ nhật, hình vuông.
Cách giải:
Đáp án A sai vì: Trong hình thoi các góc đối bằng nhau.
Chọn A.
Câu 11
Hướng dẫn:
Vận dụng các đặc điểm của hình chữ nhật
Cách giải:
Bốn góc của hình chữ nhật bằng nhau và bằng \({90^0}\)
Chọn C.
Câu 12
Hướng dẫn:
Vận dụng các đặc điểm của hình lục giác đều.
Cách giải:
Các góc bằng nhau và bằng \({120^0}\).
Chọn C.
Phần II: Tự luận
Bài 1
Hướng dẫn:
Hai cách viết tập hợp:
– Cách 1: Liệt kê các phần tử có trong tập hợp.
– Cách 2: Mô tả đặc trưng của các phần tử có trong tập hợp.
Cách giải:
Cách 1: \(B = \left\{ {0;1;2;3;4;5;6;7} \right\}\)
Cách 2: \(B = \left\{ {x \in \mathbb{N}\left| {x \le 7} \right.} \right\}\)
Bài 2
Hướng dẫn:
Vận dụng kiến thức về thứ tự thực hiện phép tính:
– Với biểu thức không có dấu ngoặc: Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ
– Với biểu thức có dấu ngoặc: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Cách giải:
|
a) \({9^2} – 64:{2^3}\) \(\begin{array}{l} = 81 – 64:8\\ = 81 – 8\\ = 73\end{array}\) |
b) \(376:\left[ {120 – \left( {{6^2} – 2.5} \right)} \right]\) \(\begin{array}{l} = 376:\left[ {120 – \left( {36 – 10} \right)} \right]\\ = 376:\left( {120 – 26} \right)\\ = 376:94\\ = 4\end{array}\) |
Bài 3
Hướng dẫn:
Áp dụng tính chất chia hết của một tổng: “Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó”.
a) Vận dụng dấu hiệu chia hết cho \(9\).
b) Vận dụng dấu hiệu chia hết cho \(3\).
Cách giải:
a) Ta có: \(\left\{ \begin{array}{l}2021\cancel{ \vdots }9\\54 \vdots 9\end{array} \right.\) nên \(\left( {2021 + 54} \right)\cancel{ \vdots }9\) (tính chất chia hết của một tổng)
b) Vì \(48 \vdots 3\) nên để \(\left( {x + 48} \right) \vdots 3\) thì \(x \vdots 3\)
Mà \(x\) thuộc tập hợp \(\left\{ {12;15;26;43;18} \right\}\)nên \(x \in \left\{ {12;15;18} \right\}\)
Vậy \(x \in \left\{ {12;15;18} \right\}\) thì tổng \(\left( {x + 48} \right) \vdots 3\).
Bài 4
Hướng dẫn:
Gọi \(a\) là số đội nhiều nhất có thể chia (điều kiện \(a \in {\mathbb{N}^*}\))
Phân tích các số ra thừa số nguyên tố
Xác định ƯCLN
Kết luận
Cách giải:
Gọi \(a\) là số đội nhiều nhất có thể chia (điều kiện \(a \in {\mathbb{N}^*}\))
Theo đề bài, ta có: \(54 \vdots a\) và \(90 \vdots a\)
Vì \(a\) là lớn nhất nên \(a\) là ƯCLN\(\left( {54,90} \right)\)
Ta có: \(54 = {2.3^3}\)
\(90 = {2.3^2}.5\)
ƯCLN\(\left( {54,90} \right) = {2.3^2} = 2.9 = 18\)
Vậy số đội có thể chia nhiều nhất là \(18\) đội.
Bài 5
Hướng dẫn:
Vận dụng các đặc điểm của hình lục giác đều, hình tam giác đều, hình thoi và hình thang cân.
Cách giải:
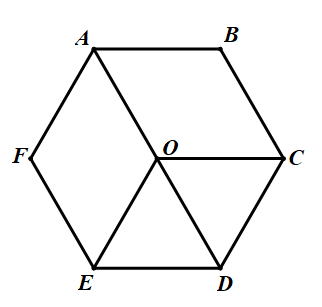
– Hình lục giác đều: \(ABCDEF\)
– Hình tam giác đều: \(OCD;OED\)
– Hình thoi: \(OABC;OCDE;OEFA\)
– Hình thang cân: \(ABCD;ADEF\)
Bài 6
Hướng dẫn:
a) Chia diện tích mảnh vườn thành các hình đã được học để tính diện tích
Áp dụng công thức tính diện tích hình chữ nhật
b) Tính diện tích của một viên gạch áp dụng công thức tính diện tích hình vuông
Tính số viên gạch để lát sân
Cách giải:
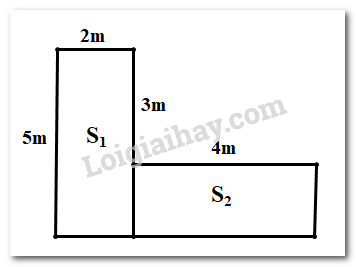
a) Gọi diện tích của mảnh vườn là \(S\)
Chia mảnh vườn thành hai phần như hình vẽ, khi đó diện tích của mảnh \({S_1}\) và \({S_2}\)
+ Tính \({S_1}\)
Chiều rộng của \({S_1}\) là: \(2m\)
Diện tích của \({S_1}\) là: \(2.5 = 10\left( {{m^2}} \right)\)
+ Tính \({S_2}\)
Chiều rộng của \({S_2}\) là: \(5 – 3 = 2\left( m \right)\)
Diện tich của \({S_2}\) là \(4.2 = 8\left( {{m^2}} \right)\)
Diện tích của mảnh vườn là: \(S = {S_1} + {S_2} = 10 + 8 = 18\left( {{m^2}} \right)\)
b) Diện tích của một viên gạch là:
\(30.30 = 900\left( {c{m^2}} \right) = 0,09\left( {{m^2}} \right)\)
Số viên gạch dùng để lát sân là:
\(18:0,09 = 200\) (viên gạch)
Bài 7
Hướng dẫn:
Gọi số bị chia là \(a\), số chia là \(b\,\,\left( {a,\,\,b \in {\mathbb{N}^ * }} \right)\).
Sử dụng: Số bị chia = Số chia . Thương + Số dư
Số dư luôn nhỏ hơn số chia
Cách giải:
Gọi số bị chia là \(a\), số chia là \(b\,\,\left( {a,\,\,b \in {\mathbb{N}^ * }} \right)\).
Vì phép chia có số dư bằng \(47\) nên \(b > 47\).
Nếu \(b = 48\) thì \(a = 48.82 + 47 = 3983 < 4000\) (thỏa mãn)
Nếu \(b \ge 49\) thì \(a \ge 48.82 + 47 = 4065 > 4000\) (không thỏa mãn)
Vậy số chia bằng \(48\).