Hướng dẫn cách giải/trả lời Đề thi giữa kì 1 Toán 6 – Đề số 10 – Chân trời sáng tạo – Đề thi giữa kì 1 – Đề số 10 – Đề thi đề kiểm tra Toán lớp 6 Chân trời sáng tạo. Phần trắc nghiệm (3 điểm) Câu 1. Biết (mathbb{N}) là tập hợp số tự nhiên….
Đề thi:
Phần trắc nghiệm (3 điểm)
Câu 1. Biết \(\mathbb{N}\) là tập hợp số tự nhiên. Cách viết đúng là
|
A. \(\mathbb{N} = \left\{ {1;2;3;4;….} \right\}\) |
B. \(\mathbb{N} = \left\{ {0;1;2;3;4;….} \right\}\) |
|
C. \(\mathbb{N} = \left\{ {0;1;2;3;4} \right\}\) |
D. \(\mathbb{N} = \left\{ {1;2;3;4} \right\}\) |
Câu 2. Phần tử thuộc tập hợp \(Q = \left\{ {0;2;4;6;8} \right\}\) là
|
A. 0 |
B. 1 |
|
C. 3 |
D. 5 |
Câu 3. Kết quả của phép tính \(12 + 8.5\) bằng
|
A. \(100\) |
B. \(52\) |
|
C. \(25\) |
D. \(136\) |
Câu 4. Biểu thức sử dụng đúng thứ tự các dấu ngoặc là
|
A. \(24:\left\{ {15 – \left[ {1 + \left( {36:18} \right)} \right]} \right\}\) |
B. \(24:\left[ {15 – \left\{ {1 + \left( {36:18} \right)} \right\}} \right]\) |
|
C. \(24:\left\{ {15 – \left( {1 + \left[ {36:18} \right]} \right)} \right\}\) |
D. \(24:\left( {15 – \left\{ {1 + \left[ {36:18} \right]} \right\}} \right)\) |
Câu 5. Trong các khẳng định sau, khẳng định nào đúng
|
A. \(3\, \vdots \,12\) |
B. \(12\,\not {\vdots} \,3\) |
|
C. \(12\, \vdots \,3\) |
D. \(12\,\not {\vdots} \,12\) |
Câu 6. Trong các số: 2; 3; 16; 18, bội của số 6 là số
|
A. 2 |
B. 3 |
|
C. 16 |
D. 18 |
Câu 7. Ghép mỗi ý ở cột A với một ý ở cột B để được khẳng định đúng và ghi vào bài làm
|
A |
B |
|
1. Số 3 là |
a. 12 : 4 |
|
2. Số 20 là |
b. \(q = 50;r = 13\) |
|
3. Thương \(q\) và số dư \(r\) trong phép chia \(a = 713\) cho \(b = 51\) là: |
c. 15 : 7 |
|
4. 8 là dư trong phép chia |
d. số nguyên tố |
|
e. \(q = 13;r = 50\) |
|
|
f. hợp số |
1 – ……; 2 – ……; 3 – ……; 4 – …….
Câu 8. Trong các hình sau, hình nào có hình ảnh là tam giác đều?

|
A. Hình 1. |
B. Hình 2. |
|
C. Hình 3. |
D. Hình 4. |
Câu 9. Có bao nhiêu hình lục giác đều trong bức ảnh sau?

|
A. 8 |
B. 7 |
|
C. 6 |
D. 5 |
Phần tự luận (7 điểm)
Bài 1 (1 điểm). Em hãy
a) Viết lại số La Mã \(XXVII\) về số tự nhiên.
b) Viết số tự nhiên nhỏ nhất có ba chữ số.
Bài 2 (2 điểm). Thực hiện phép tính (tính hợp lí nếu có thể)
|
a. \(303 – 3.\left\{ {\left[ {655 – \left( {18:2 + 1} \right){{.4}^3} + 5} \right]} \right\}:{10^0}\) |
b. 75.68 + 75.54 – 75.22 |
Bài 3 (1 điểm). Để chuẩn bị cho hội khỏe Phù Đổng, thầy huấn luyện viên của trường muốn chia đội tuyển thành các nhóm để tập thì thấy rằng nếu chia hai người một nhóm hay ba người một nhóm thì vừa đủ còn nếu chia năm người một nhóm thì lại thừa ra một người. Em hãy hộ thầy huấn luyện viên tính xem đội tuyển có bao nhiêu người. Biết rằng số vận động viên của đội tuyển có từ 30 đến 40 người.
Bài 4 (2 điểm).
a) Cho hình vuông ABCD có độ dài cạnh AB = 8 cm. Vậy độ dài cạnh CD bằng bao nhiêu?
b) Em hãy nêu các nhận xét về các cạnh của hình chữ nhật EFGH.
Bài 5 (1 điểm). Năm 2017 gạo ST 24 của Sóc Trăng – Việt Nam đã được vinh danh trong “top 3 gạo ngon nhất thế giới”. Bác Hai trồng giống lúa ST 24 đó trên một thửa ruộng hình chữ nhật có chiều dài bằng 42 m và chiều rộng bằng 25 m. Biết cứ 1 mét vuông thu hoạch được 1 kg thóc và mỗi kg thóc bác bán được 8 500 đồng. Hỏi khi bán cả thửa ruộng bác Hai thu được bao nhiêu tiền?
——– Hết ——–
Đáp án Đề thi:
Phần trắc nghiệm
|
Câu 1: B |
Câu 2: A |
Câu 3: B |
Câu 4: A |
Câu 5: C |
|
Câu 6: D |
Câu 7: 1 – d; 2 – f; 3 – e; 4 – c. |
Câu 8: A |
Câu 9: C |
|
Câu 1. Biết \(\mathbb{N}\) là tập hợp số tự nhiên. Cách viết đúng là
|
A. \(\mathbb{N} = \left\{ {1;2;3;4;….} \right\}\) |
B. \(\mathbb{N} = \left\{ {0;1;2;3;4;….} \right\}\) |
|
C. \(\mathbb{N} = \left\{ {0;1;2;3;4} \right\}\) |
D. \(\mathbb{N} = \left\{ {1;2;3;4} \right\}\) |
Hướng dẫn:
Dựa vào cách viết tập hợp và phần tử.
Lời giải
Cách viết tập hợp \(\mathbb{N}\) là: \(\mathbb{N} = \left\{ {0;1;2;3;4;….} \right\}\)
Đáp án A.
Câu 2. Phần tử thuộc tập hợp \(Q = \left\{ {0;2;4;6;8} \right\}\) là
|
A. 0 |
B. 1 |
|
C. 3 |
D. 5 |
Hướng dẫn:
Dựa vào cách mô tả tập hợp.
Lời giải
Phần tử 0 thuộc tập hợp Q nên ta chọn A.
Đáp án A.
Câu 3. Kết quả của phép tính \(12 + 8.5\) bằng
|
A. \(100\) |
B. \(52\) |
|
C. \(25\) |
D. \(136\) |
Hướng dẫn:
Dựa vào quy tắc tính với số tự nhiên.
Lời giải
Ta có: 12 + 8.5 = 12 + 40 = 52.
Đáp án B.
Câu 4. Biểu thức sử dụng đúng thứ tự các dấu ngoặc là
|
A. \(24:\left\{ {15 – \left[ {1 + \left( {36:18} \right)} \right]} \right\}\) |
B. \(24:\left[ {15 – \left\{ {1 + \left( {36:18} \right)} \right\}} \right]\) |
|
C. \(24:\left\{ {15 – \left( {1 + \left[ {36:18} \right]} \right)} \right\}\) |
D. \(24:\left( {15 – \left\{ {1 + \left[ {36:18} \right]} \right\}} \right)\) |
Hướng dẫn:
Dựa vào thứ tự dấu ngoặc.
Lời giải
Thứ tự dấu ngoặc tự nhỏ đến lớn là: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\) nên ta chọn đáp án A.
Đáp án A.
Câu 5. Trong các khẳng định sau, khẳng định nào đúng
|
A. \(3\, \vdots \,12\) |
B. \(12\,\not {\vdots} \,3\) |
|
C. \(12\, \vdots \,3\) |
D. \(12\,\not {\vdots} \,12\) |
Hướng dẫn:
Dựa vào dấu hiệu chia hết.
Lời giải
Vì 12 chia hết cho 3 nên ta chọn C.
Đáp án C.
Câu 6. Trong các số: 2; 3; 16; 18, bội của số 6 là số
|
A. 2 |
B. 3 |
|
C. 16 |
D. 18 |
Hướng dẫn:
Dựa vào kiến thức về bội của một số.
Lời giải
Bội của 6 là: B(6) = {0; 6; 12; 18; 24; 30; …} nên chỉ có 18 là bội số của 6.
Đáp án D.
Câu 7. Ghép mỗi ý ở cột A với một ý ở cột B để được khẳng định đúng và ghi vào bài làm
|
A |
B |
|
1. Số 3 là |
a. 12 : 4 |
|
2. Số 20 là |
b. \(q = 50;r = 13\) |
|
3. Thương \(q\) và số dư \(r\) trong phép chia \(a = 713\) cho \(b = 51\) là |
c. 15 : 7 |
|
4. 8 là dư trong phép chia |
d. số nguyên tố |
|
e. \(q = 13;r = 50\) |
|
|
f. hợp số |
1 – ……; 2 – ……; 3 – ……; 4 – …….
Hướng dẫn:
Dựa vào quy tắc chia với số tự nhiên.
Lời giải
1. Số 3 là số nguyên tố nên 1 – d.
2. Số 20 là hợp số nên 2 – f.
3. Ta có:
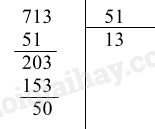
Thương \(q\) và số dư \(r\) trong phép chia \(a = 713\) cho \(b = 51\) là q = 13; r = 50 nên 3 – e.
4. Ta có 15 : 7 = 1 (dư 8) suy ra 8 là dư trong phép chia 15:7 nên 4 – c.
Đáp án 1 – d; 2 – f; 3 – e; 4 – c.
Câu 8. Trong các hình sau, hình nào có hình ảnh là tam giác đều?

|
A. Hình 1. |
B. Hình 2. |
|
C. Hình 3. |
D. Hình 4. |
Hướng dẫn:
Dựa vào kiến thức về các hình đã học.
Lời giải
Hình 1 là tam giác đều.
Đáp án A.
Câu 9. Có bao nhiêu hình lục giác đều trong bức ảnh sau?

|
A. 8 |
B. 7 |
|
C. 6 |
D. 5 |
Hướng dẫn:
Quan sát hình ảnh.
Lời giải
Các hình lục giác đều là:

Vậy có tất cả 6 hình lục giác đều trong bức ảnh.
Đáp án C.
Phần tự luận.
Bài 1 (1 điểm). Em hãy
a) Viết lại số La Mã \(XXVII\) về số tự nhiên.
b) Viết số tự nhiên nhỏ nhất có ba chữ số.
Hướng dẫn:
a) Dựa vào kiến thức về số La Mã.
b) Dựa vào kiến thức về số tự nhiên.
Lời giải
Ta có: XXVII = 27
Số tự nhiên nhỏ nhất có ba chữ số là: 100.
Bài 2 (2 điểm). Thực hiện phép tính (tính hợp lí nếu có thể)
|
a. \(303 – 3.\left\{ {\left[ {655 – \left( {18:2 + 1} \right){{.4}^3} + 5} \right]} \right\}:{10^0}\) |
b. 75.68 + 75.54 – 75.22 |
Hướng dẫn:
Sử dụng quy tắc tính với số tự nhiên và lũy thừa.
Lời giải
|
a. \(303 – 3.\left\{ {\left[ {655 – \left( {18:2 + 1} \right){{.4}^3} + 5} \right]} \right\}:{10^0}\) = 16. \(\begin{array}{l} = 303 – 3.\left\{ {655 – 10.64 + 5} \right\}:1\\ = 303 – 3.\left\{ {655 – 640 + 5} \right\}\\ = 303 – 3.20\\ = 303 – 60\\ = 243\end{array}\) |
b. 75.68 + 75.54 – 75.22 = 75(68 + 54 – 22) = 75.100 = 7500 |
Bài 3 (1 điểm). Để chuẩn bị cho hội khỏe Phù Đổng, thầy huấn luyện viên của trường muốn chia đội tuyển thành các nhóm để tập thì thấy rằng nếu chia hai người một nhóm hay ba người một nhóm thì vừa đủ còn nếu chia năm người một nhóm thì lại thừa ra một người. Em hãy hộ thầy huấn luyện viên tính xem đội tuyển có bao nhiêu người. Biết rằng số vận động viên của đội tuyển có từ 30 đến 40 người.
Hướng dẫn:
Vì nếu chia hai người một nhóm hay ba người một nhóm thì vừa đủ còn nếu chia năm người một nhóm thì lại thừa ra một người nên số vận động viên chia hết cho 2, 3 và chia 5 dư 1.
Lời giải
Vì khi chia hai người một nhóm vừa đủ nên số vận động viên chia hết cho 2.
Đội tuyển có từ 30 đến 40 người, từ số 30 đến số 40 có các chia hết cho 2 là: 30; 32; 34; 36; 38; 40
Do đó số vận động viên của đội có thể là 30; 32; 34; 36; 38 hoặc 40 người.
Khi chia ba người một nhóm cũng vừa đủ nên số vận động viên là số cũng chia hết cho 3.
Trong các số 30; 32; 34; 36; 38 số chia hết cho 3 là 30; 36. Vậy số vận động viên có thể là 30 hoặc 36 người.
Mà khi chia năm người một nhóm thì thừa 1 người nên số vận động viên là số chia cho 5 dư 1.
Trong các số 30; 36, số chia cho 5 dự 1 là số 36
Vậy số vận động viên của đội tuyển là 36 người.
Bài 4 (2 điểm).
a) Cho hình vuông ABCD có độ dài cạnh AB = 8 cm. Vậy độ dài cạnh CD bằng bao nhiêu?
b) Em hãy nêu các nhận xét về các cạnh của hình chữ nhật EFGH.
Hướng dẫn:
a) Dựa vào tính chất của hình vuông.
b) Dựa vào tính chất của hình chữ nhật.
Lời giải

a) Vì ABCD là hình vuông nên AB = CD
Mà AB = 8 cm nên CD = 8 cm.

b) Hình chữ nhật EFGH có các nhận xét về cạnh sau:
– Hai cạnh đối bằng nhau: EF = GH; EH = FG
– Hai cạnh đối EF và GH; EH và FG song song với nhau.
Bài 5 (1 điểm). Năm 2017 gạo ST 24 của Sóc Trăng – Việt Nam đã được vinh danh trong “top 3 gạo ngon nhất thế giới”. Bác Hai trồng giống lúa ST 24 đó trên một thửa ruộng hình chữ nhật có chiều dài bằng 42 m và chiều rộng bằng 25 m. Biết cứ 1 mét vuông thu hoạch được 1 kg thóc và mỗi kg thóc bác bán được 8 500 đồng. Hỏi khi bán cả thửa ruộng bác Hai thu được bao nhiêu tiền?
Hướng dẫn:
Tính diện tích thửa ruộng hình chữ nhật.
Số tiền thu được = diện tích thửa ruộng . số kg thóc bán được.
Lời giải
Vì mảnh ruộng có dạng hình chữ nhật nên diện tích của thửa ruộng là:
42 . 25 = 1050 (m2)
Vì cứ 1 mét vuông thu hoạch được 1 kg thóc nên số kg thóc thu hoạch được là:
1050 . 1 = 1050 (kg)
Vì mỗi kg thóc bán được 8 500 đồng nên số tiền bác Hai thu được là:
8 500 . 1050 = 8 925 000 (đồng).
Vậy khi bán cả thửa ruộng bác Hai thu được 8 925 000 (đồng).