Hướng dẫn giải Lời giải Đề thi học kì 1 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 6 Cánh diều.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm
|
1. C |
2. C |
3. C |
4. D |
5. D |
6. B |
7. C |
8. C |
9. A |
10. C |
Câu 1
Hướng dẫn:
Nhận biết được các tính chất của phép cộng, phép trừ, phép nhân của các số nguyên và quy tắc dấu ngoặc.
Cách giải:
+) \(a – b – c = a – \left( {b + c} \right)\) là biến đổi đúng nên đáp án A loại
+) \(a – \left( {b – c} \right) = a – b + c\)là biến đổi đúng nên đáp án B loại
+) \(a – \left( {b – c} \right) = a – b – c\) là biến đổi sai vì phá ngoặc biểu thức đẳng trước có dấu trừ, ta phải đổi dấu của các hạng tử ở trong ngoặc nên đáp án C chọn
+) \(a – \left( { – b} \right) = a + b\) là biến đổi đúng nên đáp án D loại
Chọn C.
Câu 2
Hướng dẫn:
Sử dụng phương pháp liệt kê các phần tử của một tập hợp: Liệt kê các phần tử của tập hợp trong dấu ngoặc { }; các phần tử được liệt kê 1 lần, theo thứ tự tùy ý; ngăn cách với nhau bằng dấu ;
Cách giải:
Tập hợp \(M = \left\{ {\left. x \right|12 \le x \le 15;x \in \mathbb{N}} \right\}\) còn được viết là: \(M = \left\{ {12;13;14;15} \right\}\).
Chọn C.
Câu 3
Hướng dẫn:
So sánh các số nguyên dương với nhau \( \to \) thứ tự giảm dần của các số nguyên dương (1).
So sánh các số nguyên âm với nhau \( \to \) thứ tự giảm dần của các số nguyên âm (2).
Từ (1) và (2), ta có thứ tự giảm dần của các số trong dãy.
Chú ý:
+ Các số nguyên dương luôn lớn hơn \(0\) và các số nguyên âm.
+ Các bước so sánh số nguyên âm:
– Bước 1: Bỏ dấu “\( – \)” trước cả hai số.
– Bước 2: Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu
“\( – \)”) lớn hơn.
Cách giải:
+ So sánh số nguyên dương: \(5\,;\,\,12\)
Ta có: \(12 > 5\) (1)
+ So sánh các số nguyên âm: \( – 4\,;\, – 98\,;\, – 100\)
Vì \(4 < 98 – 98 > – 100\) (2)
Từ (1) và (2), ta có: \(12 > 5 > – 4 > – 98 > – 100\)
Vậy thứ tự giảm dần của các số là: \(12\,;\,5\,;0\,; – 4\,; – 98\,; – 100\)
Chọn C.
Câu 4
Hướng dẫn:
Bước 1: Tìm bội chung nhỏ nhất của ba số tự nhiên bằng cách phân tích các số thành tích các thừa số nguyên tố.
Bước 2: Bội chung của ba số tự nhiên là bội của BCNN mới tìm được.
Cách giải:
Ta có: \(4 = {2^2};12 = {2^2}.3;22 = 2.11 \Rightarrow BCNN\left( {4,12,22} \right) = {2^2}.3.11 = 132\).
\( \Rightarrow BC\left( {4,12,22} \right) = B\left( {132} \right) = \left\{ {0;132;264;396;528;660;792;924;1056;1188;…} \right\}\).
Suy ra tập hợp các bội chung của \(4;12;22\) mà lớn hơn \(500\) và nhỏ hơn \(1000\) là: \(\left\{ {528;660;792;924} \right\}\).
Vậy có \(4\) bội chung của \(4;12;22\) mà lớn hơn \(500\) và nhỏ hơn \(1000\).
Chọn D.
Câu 5
Hướng dẫn:
+ Áp dụng quy tắc chuyển vế, tính chất của phép cộng, trừ, nhân của số nguyên để thực hiện tính toán.
+ Xác định vai trò của \(x\) để tính toán.
Cách giải:
\(\begin{array}{l}4x + 6.\left( { – 125} \right) = 2.\left( { – 125} \right)\\4x = 2.\left( { – 125} \right) – 6.\left( { – 125} \right)\\4x = \left( {2 – 6} \right).\left( { – 125} \right)\end{array}\)
\(\begin{array}{l}4x = \left( { – 4} \right).\left( { – 125} \right)\\4x = 4.125\\x = 125\end{array}\)
Vậy \(x = 125\)
Chọn D.
Câu 6
Hướng dẫn:
Sử dụng dấu hiệu chia hết cho \(3\).
Cách giải:
Ta có: \(\overline {53×7} \vdots 3 \Rightarrow \left( {5 + 3 + x + 7} \right) \vdots 3 \Rightarrow \left( {15 + x} \right) \vdots 3 \Rightarrow x \vdots 3 \Rightarrow x \in \left\{ {0;3;6;9} \right\}\).
Vậy có \(4\) giá trị của \(x\) thỏa mãn yêu cầu đề bài.
Chọn B.
Câu 7
Hướng dẫn:
Áp dụng quy tắc cộng hai số nguyên khác dấu:
+ Bước 1: Bỏ dấu “\( – \)” trước số nguyên âm, giữ nguyên số còn lại
+ Bước 2: Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn
+ Bước 3: Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở bước 2, ta có tổng cần tìm.
Cách giải:
Ta có: 6 tháng = 2 quý
Sau 6 tháng đầu năm, lợi nhuận của công ty Đại Lộc là: \( – 60 + 40 = – \left( {60 – 40} \right) = – 20\) (triệu)
Chọn C.
Câu 8
Hướng dẫn:
Đếm số tam giác đều.
Cách giải:
– Các tam giác đều cạnh 1 là: 9 tam giác
– Các tam giác đều cạnh 2 là: 3 tam giác
– Các tam giác đều cạnh 3 là: 1 tam giác
Vậy có \(9 + 3 + 1 = 13\) tam giác đều trong hình vẽ.
Chọn C.
Câu 9
Hướng dẫn:
Sử dụng định nghĩa đối xứng trục
Cách giải:
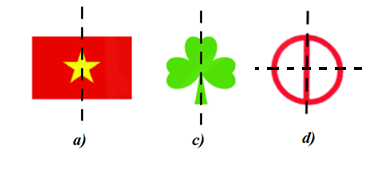
Nhận thấy hình a, c, d có trục đối xứng.
Chọn A.
Câu 10
Hướng dẫn:
Sử dụng công thức tính diện tích hình chữ nhật có độ dài hai cạnh lần lượt là \(a,b\) thì \(S = a.b\), tính được chiều dài của hình chữ nhật.
Tính được chu vi của hình chữ nhật: \(C = 2.\left( {a + b} \right)\)
Cách giải:
Chiều dài của hình chữ nhật là: \(3600:40 = 90\,\left( m \right)\)
Chu vi của hình chữ nhật là: \(2.\left( {90 + 40} \right) = 2.130 = 260\,\left( m \right)\)
Chọn C.
Phần II: Tự luận
Bài 1
Hướng dẫn:
Biểu thức có ngoặc thực hiện theo thứ tự \(\left( {\,\,\,} \right) \to \left[ {\,\,\,} \right] \to \left\{ {\,\,\,} \right\}\)
Vận dụng quy tắc bỏ ngoặc có dấu “\( – \)” ở trước.
Thực hiện các phép toán với số nguyên.
Vận dụng kiến thức lũy thừa của một số tự nhiên.
Cách giải:
|
a) \(9.2.23 + 18.32 + 3.9.30\) \(\begin{array}{l} = 18.23 + 18.32 + 3.9.5.6\\ = 18.23 + 18.32 + 18.45\\ = 18.\left( {23 + 32 + 45} \right)\\ = 18.100\\ = 1800\end{array}\) |
b) \({3^8}:{3^5} + {2023^0} – {\left( {100 – 95} \right)^2}\) \(\begin{array}{l} = {3^{8 – 5}} + 1 – {5^2}\\ = {3^3} + 1 – 25\\ = 27 + 1 – 25\\ = 3\end{array}\) |
Bài 2
Hướng dẫn:
a) Thực hiện các phép toán với số tự nhiên.
b) Vận dụng kiến thức lũy thừa với số mũ tự nhiên
Hai lũy thừa cùng cơ số bằng nhau khi số mũ của chúng bằng nhau.
Cách giải:
|
a) \(11.\left( {x – 9} \right) = 77\) \(\begin{array}{l}x – 9 = 77:11\\x – 9 = 7\\x = 7 + 9\\x = 16\end{array}\) Vậy \(x = 16\) |
b) \({2^x} + {2^{x + 4}} = 136\) \(\begin{array}{l}{2^x} + {2^x}{.2^4} = 136\\{2^x}.\left( {1 + 16} \right) = 136\\{2^x}.17 = 136\end{array}\) \(\begin{array}{l}{2^x} = 136:17\\{2^x} = 8\\{2^x} = {2^3}\\x = 3\end{array}\) Vậy \(x = 3\) |
Bài 3
Hướng dẫn:
Gọi số học sinh là \(x\,\,\left( {x \in {\mathbb{N}^*},x < 1000} \right)\) (học sinh)
Từ đề bài, suy ra \(\left( {x – 15} \right) \in {\rm{BC}}\left( {20,25,30} \right)\)
Thực hiện phân tích các số \(20;25;30\) ra thừa số nguyên tố, từ đó tìm được BCNN\(\left( {20;25;30} \right)\)
Từ đó tìm được \(x\)
Cách giải:
Gọi số học sinh của trường đó là \(x\,\,\left( {x \in {\mathbb{N}^*},x < 1000} \right)\) (học sinh)
Theo đề bài, ta có: \(x\,\, \vdots \,\,41\) và \(x\) chia \(20;25;30\) dư \(15\)
\( \Rightarrow \left( {x – 15} \right)\,\, \vdots \,\,20,25,30\) và \(x\,\, \vdots \,\,41\)
\( \Rightarrow \left( {x – 15} \right) \in {\rm{BC}}\left( {20,25,30} \right)\)
Ta có: \(\left\{ \begin{array}{l}20 = {2^2}.5\\25 = {5^2}\\30 = 2.3.5\end{array} \right. \Rightarrow {\rm{BCNN}}\left( {20,25,30} \right) = {2^2}{.5^2}.3 = 300\)
\( \Rightarrow \left( {x – 15} \right) \in {\rm{B}}\left( {300} \right) = \left\{ {0;300;600;900;1200;…} \right\}\)
\( \Rightarrow x \in \left\{ {15;315;615;915;1215;…} \right\}\)
Vì \(x\,\, \vdots \,\,41 \Rightarrow x = 615\) (thỏa mãn)
Vậy số học sinh của trường đó là \(615\).
Bài 4
Hướng dẫn:
Sử dụng công thức tính diện tích hình chữ nhật: S = a.b trong đó, a, b là chiều dài và chiều rộng của hình chữ nhật.
Cách giải:
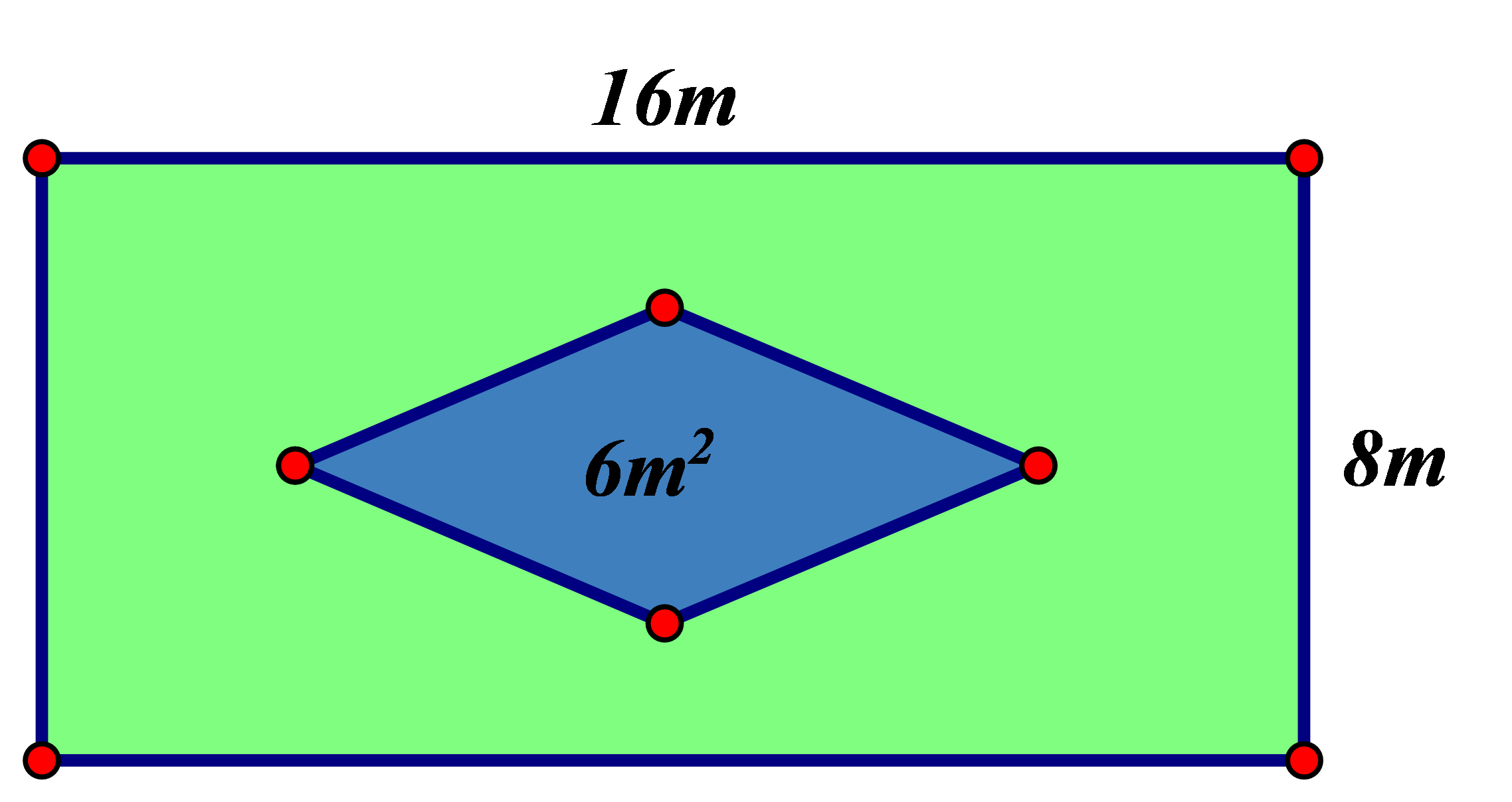
a) Diện tích của hình chữ nhật là: \(16.8 = 128\left( {{m^2}} \right)\)
Diện tích của bãi cỏ là: \(128 – 6 = 122\left( {{m^2}} \right)\)
b) Số tiền công ty phải bỏ ra để phủ kín bãi cỏ là: \(122.250\,000 = 30\,500\,000\) (đồng)
Vậy diện tích của bãi cỏ là \(122{m^2}\) và số tiền công ty phải bỏ ra để phủ kín bãi cỏ là \(30\,500\,000\) đồng.
Bài 5
Hướng dẫn:
Phân tích số nguyên \(a\left( {a > 0} \right)\) thành tích hai số nguyên cùng dấu bằng các cách có thể, từ đó tìm được \(x;y\).
Cách giải:
Ta có: \(7 = 1.7 = \left( { – 1} \right).\left( { – 7} \right)\)
Ta có bảng giá trị sau:
|
\(x – 2\) |
\( – 7\) |
\( – 1\) |
\(1\) |
\(7\) |
|
\(y + 1\) |
\( – 1\) |
\( – 7\) |
\(7\) |
\(1\) |
|
\(x\) |
\( – 5\) |
\(1\) |
\(3\) |
\(9\) |
|
\(y\) |
\( – 2\) |
\( – 8\) |
\(6\) |
\(0\) |
Vậy các cặp số \((x;y)\) là: \(\left( { – 5; – 2} \right),\left( {1; – 5} \right),\left( {3;6} \right),\left( {9;0} \right)\).