Giải Lời giải Đề thi học kì 1 – Đề số 1 – Đề thi đề kiểm tra Toán lớp 6 Cánh diều.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm
|
1. C |
2. C |
3. A |
4. B |
5. B |
6. D |
7. A |
8. C |
9. D |
10. B |
Câu 1
Hướng dẫn:
Nhận biết các phần tử thuộc tập hợp số tự nhiên.
Cách giải:
Ta có: số \(0\) thuộc tập hợp số tự nhiên nên cách viết \(0 \in \mathbb{N}\) là cách viết đúng
Chọn C.
Câu 2
Hướng dẫn:
Vận dụng dấu hiệu chia hết cho \(2\,;\,3\,;\,5\,;\,9\).
Cách giải:
Số chia hết cho \(2\,;\,5\) có chữ số tận cùng là \(0\), nên loại đáp án A và D
Ta kiểm tra hai số \(39590\) và \(39690\)
Ta có: \(3 + 9 + 5 + 9 + 0 = 26\not \vdots 9\)
\(3 + 9 + 6 + 9 + 0 = 27\not \vdots 9\) và \(27\not \vdots 3\)
Vậy số cần tìm là: \(39690\)
Chọn C.
Câu 3
Hướng dẫn:
Vận dụng quy tắc: \({\left( {{a^m}} \right)^n} = {a^{mn}}\)
Vận dụng quy tắc chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m – n}}\,\,\left( {m \ge n} \right)\)
Cách giải:
Ta có: \({3^{15}}:{9^3} = {3^{15}}:{\left( {{3^2}} \right)^3} = {3^{15}}:{3^6} = {3^{15 – 6}} = {3^9}\)
Chọn A.
Câu 4
Hướng dẫn:
Vận dụng quy tắc bỏ ngoặc có dấu “\( – \)” ở trước, thực hiện phép trừ hai số nguyên âm.
Cách giải:
\(\begin{array}{l}x – \left( { – 199} \right) = – 1\\x + 199 = – 1\\x = \left( { – 1} \right) – 199\\x = \left( { – 1} \right) + \left( { – 199} \right)\\x = – 200\end{array}\)
Vậy \(x = – 200\)
Chọn B.
Câu 5
Hướng dẫn:
Vận dụng định nghĩa hợp số, số nguyên tố của số tự nhiên để phân được các kết quả của phép tính.
Cách giải:
Ta có:
\({5^3} – {5^2} = 125 – 25 = 100\) là hợp số nên không chọn đáp án A
\({4^2} – {3^2} = 16 – 9 = 7\) là số nguyên tố nên chọn B
\({6^2} – {3^2} = 36 – 9 = 27\) là hợp số nên không chọn đáp án C
\({5^2} – {3^2} = 25 – 9 = 16\) là hợp số nên không chọn đáp án D.
Chọn B.
Câu 6
Hướng dẫn:
Vận dụng kiến thức về số nguyên âm, số nguyên dương và số sánh các số nguyên với nhau.
Cách giải:
Vì \(6 > 5\) nên \( – 6 < – 5\) do đó đáp án D sai.
Chọn D.
Câu 7
Hướng dẫn:
Sử dụng công thức tính chu vi của hình vuông có cạnh là \(a\) là: \(P = 4.a\)
Cách giải:
Chu vi của hình vuông là: \(4.10 = 40\,\,\left( {cm} \right)\)
Chọn A.
Câu 8
Hướng dẫn:
Sử dụng công thức tính diện diện tích hình thang có độ dài hai đáy là \(a\,,\,b\) và có chiều cao là \(h\). Khi đó: \(S = \dfrac{{\left( {a + b} \right).h}}{2}\), tính diện tích của hiên nhà.
Chi phí làm hiên nhà = diện tích của hiên nhà \( \times \) chi phí của \(1\,{m^2}\)
Cách giải:
Diện tích của hiên nhà là: \(\dfrac{{\left( {14 + 36} \right).12}}{2} = 50.6 = 300\,\,\left( {{m^2}} \right)\)
Chi phí làm hiên nhà là: \(300.120\,000 = 36\,000\,000\) (đồng)
Chọn C.
Câu 9
Hướng dẫn:
Vận dụng công thức tính diện tích:
+ Hình vuông có cạnh bằng \(a\) thì \(S = a.a\)
+ Hình bình hành có độ dài hai cạnh đáy là \(a,b\), độ dài đường cao tương ứng với cạnh \(a\) là \(h\) thì \(S = a.h\).
+ Hình chữ nhật có độ dài hai cạnh là \(a,b\) thì \(S = a.b\)
+ Hình thoi có độ dài hai đường chéo \(m,n\) là \(S = \dfrac{1}{2}m.n\).
Cách giải:
Diện tích hình 1 là: \(4.4 = 16\,\left( {c{m^2}} \right)\)
Diện tích hình 2 là: \(2.5 = 10\,\left( {c{m^2}} \right)\)
Diện tích hình 3 là: \(3.4 = 12\,\left( {c{m^2}} \right)\)
Diện tích hình 4 là: \(\dfrac{1}{2}.3.6 = 9\,\left( {c{m^2}} \right)\)
Ta có: \(9 < 10 < 12 < 16\)
Vậy diện tích hình 4 là bé nhất.
Chọn D.
Câu 10
Hướng dẫn:
Vận dụng định nghĩa trục đối xứng của một hình.
Cách giải:
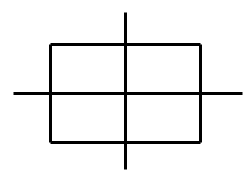
Hình chữ nhật có \(2\) trục đối xứng như hình vẽ.
Chọn B.
Phần II: Tự luận
Bài 1
Hướng dẫn:
Sử dụng thứ tự thực hiện phép tính đối với biểu thức có dấu ngoặc: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Vận dụng kiến thức lũy thừa của một số tự nhiên
Cách giải:
|
a) \(12:\left[ {450:\left( {125 + 25.4} \right)} \right]\) \(\begin{array}{l} = 12:\left[ {450:\left( {125 + 100} \right)} \right]\\ = 12:\left[ {450:225} \right]\\ = 12:2\\ = 6\end{array}\) |
b) \({4.5^2} – {3^2}.\left( {{{2015}^0} + {1^{100}}} \right)\) \(\begin{array}{l} = 4.25 – 9.\left( {1 + 1} \right)\\ = 100 – 9.2\\ = 100 – 18\\ = 82\end{array}\) |
c)
\(\begin{array}{l}98.12345 + 12345.101 + 12345\\ = 12345.\left( {98 + 101 + 1} \right)\\ = 12345.200\\ = 2469000\end{array}\)
Bài 2
Hướng dẫn:
Giải bài toán ngược để tìm \(x\)
Vận dụng kiến thức về lũy thừa với số tự nhiên, so sánh lũy thừa cùng cơ số để tìm \(x\).
Cách giải:
|
a) \(71 – \left( {33 + x} \right) = 26\) \(\begin{array}{l}33 + x = 71 – 26\\33 + x = 45\\x = 45 – 33\\x = 12\end{array}\) Vậy \(x = 12\) |
b) \({3^{4x + 1}} = {27^{x + 3}}\) \(\begin{array}{l}{3^{4x + 1}} = {3^{3\left( {x + 3} \right)}}\\4x + 1 = 3(x + 3)\\4x + 1 = 3x + 9\\4x – 3x = 9 – 1\\x = 8\end{array}\) Vậy \(x = 8\). |
Bài 3
Hướng dẫn:
a) Vận dụng quy tắc tìm ước chung lớn nhất của hai số.
b) Vận dụng quy tắc tìm bội chung nhỏ nhất của hai số.
Cách giải:
a) Vì \(x\) lớn nhất và \(480\,\, \vdots \,\,x\,;\,\,600\,\, \vdots \,\,x\) \( \Rightarrow x = \)ƯCLN\(\left( {480,600} \right)\)
Ta có: \(\left\{ \begin{array}{l}480 = {2^5}.3.5\\600 = {2^3}{.3.5^2}\end{array} \right. \Rightarrow \)ƯCLN\(\left( {480;600} \right) = {2^3}.3.5 = 120\)
Vậy \(x = 120\)
b) Vì \(x\,\, \vdots \,\,20,\,\,x\,\, \vdots \,\,35\) \( \Rightarrow x \in \)BC\(\left( {20;35} \right)\)
Ta có: \(\left\{ \begin{array}{l}20 = {2^2}.5\\35 = 5.7\end{array} \right. \Rightarrow \)BCNN\(\left( {20;35} \right) = {2^2}.5.7 = 140\)
\( \Rightarrow \)BC\(\left( {20;35} \right) = \)B\(\left( {140} \right) = \left\{ {0;140;280;420;560;…} \right\}\)
Mà \(x < 500 \Rightarrow x \in \left\{ {0;140;280;420} \right\}\)
Vậy \(x \in \left\{ {0;140;280;420} \right\}\).
Bài 4
Hướng dẫn:
Tính diện tích của hình bình hành \(ABCD\)
Tính diện của hình thang cân \(BEFC\)
\( \Rightarrow \) Tính diện tích của mảnh đất
Tính chu vi của mảnh đất: \(AE + EF + FC + CD + DA\)
Cách giải:
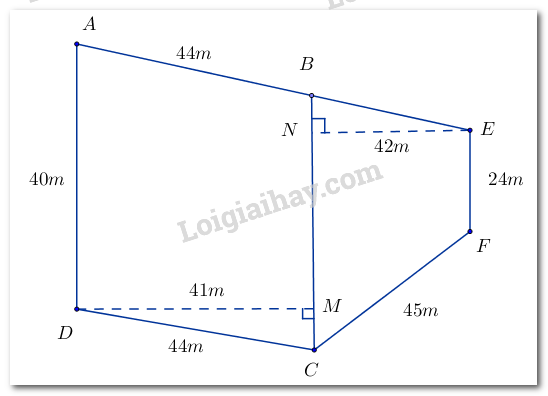
* Diện tích của hình bình hành \(ABCD\) là: \(DM.BC = 41.40 = 1640\left( {{m^2}} \right)\)
Diện tích của hình thang cân \(BEFC\) là: \(\dfrac{{\left( {EF + BC} \right).EN}}{2} = \dfrac{{\left( {24 + 40} \right).42}}{2} = 1344\left( {{m^2}} \right)\)
Diện tích của mảnh đất là: \(1640 + 1344 = 2984\left( {{m^2}} \right)\)
* Ta có: \(AB = CD = 44\left( m \right);BE = CF = 45\left( m \right)\)
Chu vi của mảnh đất là: \(AE + EF + FC + CD + DA\)
\(\begin{array}{l} = AB + BE + EF + FC + CD + DA\\ = 44 + 45 + 24 + 45 + 44 + 40 = 242\left( {{m^2}} \right)\end{array}\)
Bài 5
Hướng dẫn:
Sử dụng tính chất chia hết của một tích, nhóm các hạng tử để xuất hiện thừa số \(13\).
Cách giải:
\(\begin{array}{l}A\; = 1 + 3 + {3^2} + {3^{3\;}} + \ldots + {3^{11}}\\A\; = \left( {1 + 3 + {3^2}} \right) + \left( {{3^3} + {3^4} + {3^5}} \right) + \ldots + \left( {{3^9} + {3^{10}}{\rm{ + }}{3^{11}}} \right)\\A\; = \left( {1 + 3 + {3^2}} \right) + {3^3}.\left( {1 + 3 + {3^2}} \right) + \ldots + {3^9}.\left( {1 + 3 + {3^2}} \right)\\A\; = 13\; + \;{3^3}.13\; + \ldots + {3^9}.13\\A\; = 13.\left( {1 + {3^3} + \ldots + {3^9}} \right)\;\\ \Rightarrow A\,\, \vdots \,\,13\end{array}\)