Hướng dẫn giải Đề thi học kì 2 Toán 6 – Đề số 4 – Cánh diều – Đề thi học kì 2 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 6 Cánh diều. Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp…
Đề thi:
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Kết quả của phép tính \(\left( { – 76,4} \right).\left( { – 1,2} \right)\) là:
A. \( – 91,68\) B. 9,168 C. \( – 9,168\) D. 91,68
Câu 2: Tung hai đồng xu cân đối và đồng chất 20 lần ta được kết quả như bảng dưới đây:
Xác suất thực nghiệm xuất hiện sự kiện một mặt sấp, một mặt ngửa là:
A. \(\dfrac{1}{4}\) B. \(\dfrac{3}{5}\) C. \(\dfrac{3}{{20}}\) D. \(\dfrac{2}{5}\)
Câu 3: Trong các phát biểu sau, phát biểu nào sai?
a) Hai tia chung gốc \(Kp,\,Kg\) tạo thành đường thẳng \(pg\) gọi là hai tia đối nhau.
b) Hai tia trùng nhau thì phải có chung điểm gốc.
c) Hai tia có chung điểm gốc thì đối nhau.
d) Điểm \(O\) nằm giữa đường thẳng \(xy\) tạo thành hai tia \(Ox\) và \(Oy\).
A. Phát biểu a) B. Phát biểu b) C. Phát biểu c) D. Phát biểu d)
Câu 4: Góc \(xOz\) có số đo là:
A. \({120^0}\) B. \({30^0}\) C. \({40^0}\) D. \({60^0}\)
Phần II. Tự luận (8 điểm):
Bài 1 (2 điểm) Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\dfrac{{ – 7}}{{16}} + \dfrac{3}{{16}}\) b) \(\dfrac{1}{7} + \dfrac{{ – 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ – 4}}{7}\) c) \(\dfrac{4}{9}.\dfrac{{ – 7}}{{26}} + \dfrac{{45}}{{ – 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
Bài 2 (2 điểm) Tìm x biết:
a) \(x + \dfrac{3}{5} = \dfrac{1}{{10}}\) b) \(\dfrac{2}{3}:x = 2,4 – \dfrac{4}{5}\) c) \(\dfrac{5}{4}\left( {x – \dfrac{3}{5}} \right) = \dfrac{{ – 1}}{8}\)
Bài 3 (1,5 điểm) Ông \(A\) ở Gia Lai thu hoạch khoai lang để bán cho thương lái xuất khẩu sang Trung Quốc. Lần đầu ông \(A\) bán được \(\dfrac{1}{5}\) khối lượng khoai lang thu hoạch được, lần thứ hai ông bán được \(\dfrac{3}{8}\) khối lượng khoai lang còn lại. Sau hai lần bán, do Trung Quốc không mua khoai lang nữa nên ông \(A\) còn 2,5 tấn khoai lang không bán được. Nhờ chương trình “Giải cứu khoai lang cho đồng bào Gia Lai” nên ông \(A\) mới bán được nốt khối lượng khoai lang còn lại.
a) Hỏi khối lượng khoai lang ông \(A\) thu hoạch được là bao nhiêu?
b) Tính tỉ số phần trăm số tiền bán khoai lang lần thứ ba so với tổng số tiền bán khoai lang hai lần đầu. Biết rằng giá khoai lang hai lần đầu đều là 10.000 đồng/kg và giá bán khoai lang trong chương trình “Giải cứu” là
2.000 đồng/kg.
Bài 4 (2 điểm)
Vẽ đoạn thẳng \(AB = 9cm\). Lấy điểm \(C\)thuộc đoạn thẳng \(AB\) sao cho \(AC = 6cm\). Lấy điểm \(N\) nằm giữa \(A\) và \(C\) sao cho \(C\) là trung điểm của đoạn thẳng \(BN\).
a) Tính \(NC\) và \(NB\).
b) Chứng tỏ \(N\) là trung điểm của đoạn thẳng \(AC\).
Bài 5 (0,5 điểm)
Chứng tỏ \(\dfrac{{14n + 3}}{{21n + 4}}\) là phân số tối giản (\(n\) là số tự nhiên).
Đáp án Đề thi:
Phần I: Trắc nghiệm
|
1. D |
2. B |
3. C |
4. C |
Câu 1
Hướng dẫn:
Thực hiện phép nhân hai số thập phân.
Cách giải:
Ta có: \(\left( { – 76,4} \right).\left( { – 1,2} \right) = 76,4.1,2 = 91,68\)
Chọn D.
Câu 2
Hướng dẫn:
Xác suất thực nghiệm xuất hiện sự kiện một mặt sấp là, một mặt ngửa là: Số lần xuất hiện sự kiện : Tổng số lần tung.
Cách giải:
Xác suất thực nghiệm xuất hiện sự kiện một mặt sấp là, một mặt ngửa là: \(\dfrac{{12}}{{20}} = \dfrac{3}{5}\).
Chọn B.
Câu 3
Hướng dẫn:
Vẽ hình minh họa chỉ ra phát biểu c) sai.
Cách giải:
Phát biểu c) sai, chẳng hạn: Hai tia \(Ox\) và \(Oy\) có chung gốc \(O\) nhưng không đối nhau (do không tạo thành một đường thẳng)
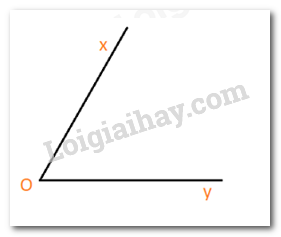
Chọn C.
Câu 4
Hướng dẫn:
Một cạnh đi qua vạch số 0 ở phía nào thì đo theo vạch ở phía ấy.
Góc nhọn có số đo nhỏ hơn \({90^0}\)
Góc tù có số đo lớn hơn \({90^0}\)
Bước 1: Đặt thước đo góc sao cho tâm của thước trùng với tâm \(O\) của góc, một cạnh của góc đi qua vạch \({0^0}\)
Bước 2: Xem cạnh thứ hai của góc đi qua vạch nào của thước, từ đó tìm được số đo của góc đó.
Cách giải:
Cạnh \(Ox\) đi qua vạch số \({0^0}\) của thước đo góc
Cạnh \(Oz\) đi qua vạch số \({60^0}\) của thước đo góc
Do đó, số đo góc \(xOz\) là \({60^0}\)
Chọn C.
Phần II: Tự luận
Bài 1
Hướng dẫn:
a) Cộng hai phân số cùng mẫu.
b) Nhóm thích hợp các phân số cùng mẫu.
c) Sử dụng tính chất phân phối của phép nhân và phép cộng.
Cách giải:
a) \(\dfrac{{ – 7}}{{16}} + \dfrac{3}{{16}}\)
\(\begin{array}{l} = \dfrac{{ – 7 + 3}}{{16}}\\ = \dfrac{{ – 4}}{{16}}\\ = \dfrac{{ – 1}}{4}\end{array}\)
b) \(\dfrac{1}{7} + \dfrac{{ – 9}}{{27}} + \dfrac{{10}}{7} + \dfrac{{ – 4}}{7}\)
\(\begin{array}{l} = \left( {\dfrac{1}{7} + \dfrac{{10}}{7} + \dfrac{{ – 4}}{7}} \right) + \dfrac{{ – 1}}{3}\\ = \dfrac{{1 + 10 – 4}}{7} + \dfrac{{ – 1}}{3}\\ = \dfrac{7}{7} + \dfrac{{ – 1}}{3}\\ = \dfrac{3}{3} + \dfrac{{ – 1}}{3}\\ = \dfrac{{3 – 1}}{3}\\ = \dfrac{2}{3}\end{array}\)
c) \(\dfrac{4}{9}.\dfrac{{ – 7}}{{26}} + \dfrac{{45}}{{ – 26}}.\dfrac{4}{9} + \dfrac{1}{3}\)
\(\begin{array}{l} = \dfrac{4}{9}.\left( {\dfrac{{ – 7}}{{26}} + \dfrac{{45}}{{ – 26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}\left( {\dfrac{{ – 7}}{{26}} + \dfrac{{ – 45}}{{26}}} \right) + \dfrac{1}{3}\\ = \dfrac{4}{9}.\dfrac{{ – 7 – 45}}{{26}} + \dfrac{1}{3}\\ = \dfrac{4}{9}.\left( { – 2} \right) + \dfrac{1}{3}\\ = \dfrac{{ – 8}}{9} + \dfrac{3}{9}\\ = \dfrac{{ – 8 + 3}}{9}\\ = \dfrac{{ – 5}}{9}\end{array}\)
Bài 2 (VD):
Hướng dẫn:
Thực hiện bài toán thứ tự thực hiện phép tính ngược để tìm x.
Cách giải:
a) \(x + \dfrac{3}{5} = \dfrac{1}{{10}}\)
\(\begin{array}{l}x = \dfrac{1}{{10}} – \dfrac{3}{5}\\x = \dfrac{1}{{10}} – \dfrac{6}{{10}}\\x = – \dfrac{5}{{10}}\\x = – \dfrac{1}{2}\end{array}\)
b) \(\dfrac{2}{3}:x = 2,4 – \dfrac{4}{5}\)
\(\begin{array}{l}\dfrac{2}{3}:x = \dfrac{{12}}{5} – \dfrac{4}{5}\\\dfrac{2}{3}:x = \dfrac{8}{5}\\\,\,\,\,\,\,\,x = \dfrac{2}{3}:\dfrac{8}{5}\\\,\,\,\,\,\,\,x = \dfrac{5}{{12}}\end{array}\)
c) \(\dfrac{5}{4}\left( {x – \dfrac{3}{5}} \right) = \dfrac{{ – 1}}{8}\)
\(\begin{array}{l}x – \dfrac{3}{5} = \dfrac{{ – 1}}{8}:\dfrac{5}{4}\\x – \dfrac{3}{5} = \dfrac{{ – 1}}{{10}}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ – 1}}{{10}} + \dfrac{3}{5}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{{ – 1}}{{10}} + \dfrac{6}{{10}}\\x\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{{10}} = \dfrac{1}{2}\end{array}\)
Bài 3 (VD):
Hướng dẫn:
Áp dụng quy tắc: Muốn tìm \(\dfrac{m}{n}{\kern 1pt} \) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {m,n \in \mathbb{N},{\kern 1pt} {\kern 1pt} n \ne 0} \right).\)
Cách giải:
a) Phân số chỉ khối lượng khoai còn lại sau khi bán lần đầu là:
\(1 – \dfrac{1}{5} = \dfrac{4}{5}\) (số khoai thu hoạch được)
Phân số chỉ số khoai bán lần thứ hai là:
\(\dfrac{3}{8}.\dfrac{4}{5} = \dfrac{3}{{10}}\) (số khoai thu hoạch được)
Cả 2 lần bán được số khoai là:
\(\dfrac{1}{5} + \dfrac{3}{{10}} = \dfrac{1}{2}\) (số khoai thu hoạch được)
Phân số chỉ số khoai còn lại sau hai lần bán là:
\(1 – \dfrac{1}{2} = \dfrac{1}{2}\) (số khoai thu hoạch được)
Khối lượng khoai lang ông A thu hoạch được là:
\(2,5:\dfrac{1}{2} = 5\) (tấn)
b) Hai lần đầu ông A bán được số ki-lô-gam khoai là:
\(\dfrac{1}{2}.5 = \dfrac{5}{2}\) (tấn)
\(\dfrac{5}{2}\) tấn \( = 2,5\) tấn \( = 2500kg\)
Tổng số tiền bán khoai lang hai lần đầu là:
\(10000.2500 = 25000000\) (đồng)
Số tiền bán khoai lang lần thứ ba là:
\(2000.2500 = 5000000\) (đồng)
Tỉ số phần trăm số tiền bán khoai lang lần thứ ba so với tổng số tiền bán khoai lang hai lần đầu là:
\(5000000:25000000.100\% {\rm{\;}} = 20\% \)
Bài 4 (VD):
Hướng dẫn:
– Vẽ đoạn thẳng khi biết độ dài
– Tính độ dài đoạn thẳng, chứng minh trung điểm.
Cách giải:
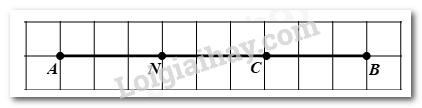
a) Do \(C\) thuộc đoạn thẳng \(AB\) nên: \(AC + CB = AB\)
\(6 + CB = 9\)
\(CB = 9 – 6 = 3cm\)
Do \(C\) là trung điểm của đoạn thẳng \(NB\) nên: \(CN = CB = 3cm\)
Do \(C\) là trung điểm của đoạn thẳng \(NB\) nên: \(BN = 2CB = 2.3 = 6cm\)
b) Do \(N\) nằm giữa \(A\) và \(C\) nên: \(AN + NC = AC\)
\(AN + 3 = 6\)
\(AN = 6 – 3 = 3cm\)
Ta có: \(AN = NC = 3cm\), \(N\) nằm giữa \(A\) và \(C\) nên \(N\) là trung điểm của đoạn thẳng \(AC\)
Bài 5 (VDC):
Hướng dẫn:
Vận dụng rút gọn phân số.
Cách giải:
Gọi \(d = \)ƯCLN\(\left( {14n + 3,21n + 4} \right)\).
Có \(14n + 3\) chia hết cho \(d\)và \(21n + 4\) chia hết cho \(d\).
Từ đó suy ra: \(3.\left( {14n + 3} \right) – 2.\left( {21n + 4} \right) = 1\) chia hết cho \(d\).
Vậy \(d = 1\) hay \(\dfrac{{14n + 3}}{{21 + 4}}\) là phân số tối giản.