Đáp án Câu hỏi 4 trang 94 SGK Toán 5 Bình Minh – Bài 73. Luyện tập. Tham khảo: Muốn tính diện tích hình tam giác ta lấy độ dài cạnh đáy nhân với chiều cao (cùng một.
Câu hỏi/Đề bài:
Số?
Cho hình thang ABCD có đáy lớn DC gấp đôi đáy bé AB.
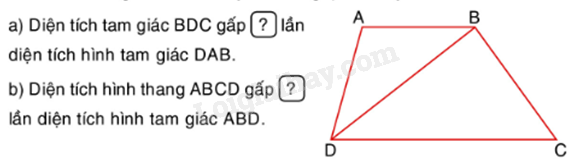
Hướng dẫn:
– Muốn tính diện tích hình tam giác ta lấy độ dài cạnh đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
– Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Lời giải:
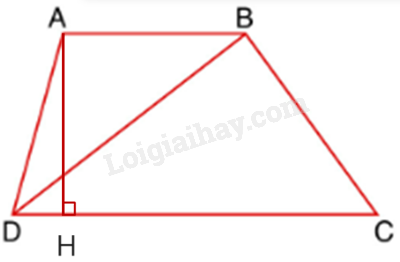
Gọi AH là đường cao của hình thang nên AH cũng là đường cao của hình tam giác BDC và ABD.
a)
Diện tích tam giác BDC bằng:
$\frac{{DC \times AH}}{2} = \frac{{(AB \times 2) \times AH}}{2} = AB \times AH$
Diện tích tam giác DAB bằng: $\frac{{AB \times AH}}{2}$
Ta có: Tỉ số giữa diện tích tam giác BDC và diệ tích tam giác DAB là:
$\left( {AB \times AH} \right):\frac{{AB \times AH}}{2} = \left( {AB \times AH} \right) \times \frac{2}{{AB \times AH}} = 2$
Vậy diện tích tam giác BDC gấp 2 lần diện tích tam giác DAB.
b)
Diện tích hình thang ABCD là:
$\frac{{\left( {AB + CD} \right) \times AH}}{2} = \frac{{(AB + AB \times 2) \times AH}}{2} = \frac{{AB \times (1 + 2) \times AH}}{2} = \frac{{AB \times 3 \times AH}}{2}$
Diện tích tam giác ABD bằng: $\frac{{AB \times AH}}{2}$
Ta có tỉ số giữa diện tích hình thang ABCD và diện tích tam giác ABD là: $\frac{{AB \times 3 \times AH}}{2}:\frac{{AB \times AH}}{2} = \frac{{AB \times 3 \times AH}}{2} \times \frac{2}{{AB \times AH}} = 3$
Vậy diện tích hình thang ABCD gấp 3 lần diện tích tam giác ABD.