Lời giải Câu hỏi Vận dụng 4 trang 37 SGK Toán 12 Kết nối tri thức – Bài 14. Phương trình mặt phẳng. Hướng dẫn: Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh.
Câu hỏi/Đề bài:
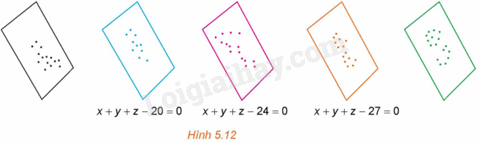
Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh của thí sinh đó.
a) Chứng minh rằng các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z – 27 = 0\).
b) Chứng minh rằng tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Hướng dẫn:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải:
a) Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_0};{y_0};{z_0}\) sao cho tổng điểm của thí sinh đó là 27. Khi đó, \({x_0} + {y_0} + {z_0} = 27\). Suy ra, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_0};y = {y_0},z = {z_0}\) vào phương trình \(x + y + z – 27 = 0\) ta có:
${{x}_{0}}+{{y}_{0}}+{{z}_{0}}-27=0\Leftrightarrow 27-27=0\left( LD \right)$
Do đó, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z – 27 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z – 27 = 0\).
b) Xét phương trình mặt phẳng (M): \(x + y + z – 24 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_1};{y_1};{z_1}\) sao cho tổng điểm của thí sinh đó là 24. Khi đó, \({x_1} + {y_1} + {z_1} = 24\). Khi đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_1};y = {y_1},z = {z_1}\) vào phương trình \(x + y + z – 24 = 0\) ta có:
${{x}_{1}}+{{y}_{1}}+{{z}_{1}}-24=0\Leftrightarrow 24-24=0\left( L \right)$
Do đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z – 24 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 24 (nếu có) cùng thuộc mặt phẳng (M).
Xét phương trình mặt phẳng (N): \(x + y + z – 20 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_2};{y_2};{z_2}\) sao cho tổng điểm của thí sinh đó là 20. Khi đó, \({x_2} + {y_2} + {z_2} = 20\). Khi đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_2};y = {y_2},z = {z_2}\) vào phương trình \(x + y + z – 20 = 0\) ta có:
${{x}_{2}}+{{y}_{2}}+{{z}_{2}}-20=0\Leftrightarrow 20-20=0\left( LD \right)$
Do đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) thuộc mặt phẳng (N).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 20 cùng thuộc mặt phẳng có phương trình (N).
Theo a, các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 cùng thuộc mặt phẳng (P) có phương trình \(x + y + z – 27 = 0\).
Ta thấy ba mặt phẳng (M), (N), (P) có vectơ pháp tuyến \(\overrightarrow n \left( {1;1;1} \right)\) và \( – 24 \ne – 20 \ne – 27\) nên ba mặt phẳng (M), (N), (P) song song với nhau.
Từ đó ta có kết luận: Tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.