Đáp án Câu hỏi Vận dụng 3 trang 36 SGK Toán 12 Kết nối tri thức – Bài 14. Phương trình mặt phẳng. Gợi ý: Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u , \overrightarrow v } \right]\).
Câu hỏi/Đề bài:
Trong không gian Oxyz, sàn của một căn phòng có dạng hình tứ giác với bốn đỉnh O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), \(C\left( {0;2\sqrt 2 ;0} \right)\). Bốn bức tường của căn phòng đều vuông góc với sàn.
a) Viết phương trình bốn mặt phẳng tương ứng chứa bốn bức tường đó.
b) Trong bốn mặt phẳng tương ứng chứa bốn bức tường đó, hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.

Hướng dẫn:
Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau:
+ Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
+ Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải:
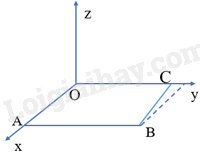
a) Bốn mặt phẳng tương ứng chứa bốn bức tường vuông góc với mặt sàn là: Mặt phẳng (Oyz), mặt phẳng (Oxz), mặt phẳng (P) chứa hai điểm A, B và vuông góc với mặt sàn, mặt phẳng (Q) chứa hai điểm B, C và vuông góc với mặt sàn.
Mặt phẳng (Oyz) có vectơ pháp tuyến \(\overrightarrow i \left( {1;0;0} \right)\) và đi qua điểm \(O\left( {0;0;0} \right)\) nên phương trình mặt phẳng (Oyz) là: \(x = 0\)
Mặt phẳng (Oxz) có vectơ pháp tuyến \(\overrightarrow j \left( {0;1;0} \right)\) và đi qua điểm \(O\left( {0;0;0} \right)\) nên phương trình mặt phẳng (Oxz) là: \(y = 0\)
Ta có: \(\overrightarrow {AB} \left( {0;3;0} \right),\overrightarrow {BC} \left( { – 2;2\sqrt 2 – 3;0} \right),\overrightarrow i \left( {1;0;0} \right),\overrightarrow j \left( {0;1;0} \right),\overrightarrow k \left( {0;0;1} \right)\)
Mặt phẳng (P) đi qua điểm A(2; 0; 0) và nhận \(\overrightarrow i = \left( {1;0;0} \right)\) làm vectơ pháp tuyến. Do đó, phương trình mặt phẳng (P) là: \(x – 2 = 0\)
\(\left[ {\overrightarrow {BC} ,\overrightarrow k } \right] = \left( {\left| {\begin{array}{*{20}{c}}{2\sqrt 2 – 3}&0\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ – 2}\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ – 2}&{2\sqrt 2 – 3}\\0&0\end{array}} \right|} \right) = \left( {2\sqrt 2 – 3;2;0} \right)\)
Mặt phẳng (Q) đi qua điểm \(C\left( {0;2\sqrt 2 ;0} \right)\) và nhận \(\left[ {\overrightarrow {BC} ,\overrightarrow k } \right] = \left( {2\sqrt 2 – 3;2;0} \right)\) làm vectơ pháp tuyến. Do đó, phương trình mặt phẳng (Q) là:
\(\left( {2\sqrt 2 – 3} \right)x + 2\left( {y – 2\sqrt 2 } \right) = 0 \Leftrightarrow \left( {2\sqrt 2 – 3} \right)x + 2y – 4\sqrt 2 = 0\)
b) Các cặp mặt phẳng vuông góc với nhau là: (Oxz) và (Oyz); (Oxz) và (P).