Lời giải Câu hỏi Luyện tập 6 trang 71 SGK Toán 12 Kết nối tri thức – Bài 8. Biểu thức tọa độ của các phép toán vectơ. Tham khảo: Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính.
Câu hỏi/Đề bài:
Trong tình huống mở đầu, hãy tính độ lớn của góc \(\alpha \).
Hướng dẫn:
Sử dụng kiến thức về cosin góc của 2 vectơ trong không gian để tính: Nếu \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x’;y’;z’} \right)\) là hai vectơ khác \(\overrightarrow 0 \) thì \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{xx’ + yy’ + zz’}}{{\sqrt {{x^2} + {y^2} + {z^2}} .\sqrt {x{‘^2} + y{‘^2} + z{‘^2}} }}\)
Lời giải:
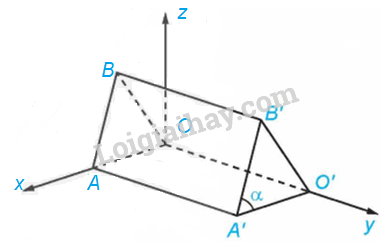
Theo Ví dụ 6 ta có: \(\overrightarrow {A’B’} = \left( { – 120;0;300} \right);\left| {\overrightarrow {A’B’} } \right| = 60\sqrt {29} cm,O’\left( {0;450;0} \right),\)\(A’\left( {240;450;0} \right)\)
Do đó, \(\overrightarrow {A’O’} = \left( { – 240;0;0} \right) \Rightarrow \left| {\overrightarrow {A’O’} } \right| = 240cm\)
Ta có: \(\cos \left( {\overrightarrow {A’B’} ;\overrightarrow {A’O’} } \right) = \frac{{\overrightarrow {A’B’} .\overrightarrow {A’O’} }}{{\left| {\overrightarrow {A’B’} } \right|.\left| {\overrightarrow {A’O’} } \right|}} = \frac{{\left( { – 120} \right)\left( { – 240} \right) + 0.0 + 300.0}}{{60\sqrt {29} .240}} = \frac{{2\sqrt {29} }}{{29}}\)
\( \Rightarrow \widehat {B’A’O’} \approx {68^0}\). Vậy \(\alpha \approx {68^0}\)