Đáp án Câu hỏi Luyện tập 6 trang 52 SGK Toán 12 Kết nối tri thức – Bài 6. Vectơ trong không gian. Hướng dẫn: Sử dụng kiến thức về hai vectơ đối nhau để chứng minh: Trong không gian.
Câu hỏi/Đề bài:
Trong Ví dụ 6, chứng minh rằng:
a) \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau;
b) \(\overrightarrow {SD} – \overrightarrow {BN} – \overrightarrow {CM} = \overrightarrow {SC} \)
Hướng dẫn:
a) Sử dụng kiến thức về hai vectơ đối nhau để chứng minh: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( – \overrightarrow a \).
b) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải:
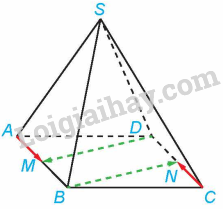
a) Tứ giác ABCD là hình bình hành nên \(AB = CD\), AB//CD. Suy ra \(BM = DN\) (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, \(BN = DM\) và BN//DM. Hai vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) có cùng độ dài và ngược hướng nên \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau.
b) Theo a ta có: \(\overrightarrow {BN} = – \overrightarrow {DM} \)
Do đó, \(\overrightarrow {SD} – \overrightarrow {BN} – \overrightarrow {CM} = \overrightarrow {SD} + \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {SM} + \overrightarrow {MC} = \overrightarrow {SC} \)