Đáp án Câu hỏi Luyện tập 5 trang 64 SGK Toán 12 Kết nối tri thức – Bài 7. Hệ trục tọa độ trong không gian. Gợi ý: Sử dụng kiến thức về thiết lập tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa.
Câu hỏi/Đề bài:
Trong Ví dụ 5, xác định tọa độ của các điểm D và D’ sao cho ABCD.A’B’C’D’ là hình hộp.
Hướng dẫn:
Sử dụng kiến thức về thiết lập tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} – {x_M};{y_N} – {y_M};{z_N} – {z_M}} \right)\).
Lời giải:
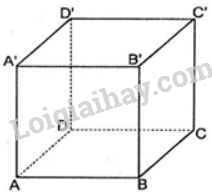
Gọi tọa độ của điểm D là (x; y; z), tọa độ của D’ là \(\left( {x’;y’;z’} \right)\), khi đó \(\overrightarrow {AD} \left( {x – 1;y;z – 2} \right)\) và \(\overrightarrow {A’D’} \left( {x – 5;y;z – 1} \right)\).
Để ABCD.A’B’C’D’ là hình hộp thì ABCD là hình bình hành.
Do đó, \(\overrightarrow {AD} = \overrightarrow {BC} \Rightarrow \left\{ \begin{array}{l}x – 1 = 4\\y = – 5\\z – 2 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = – 5\\z = 6\end{array} \right.\). Suy ra \(D\left( {5; – 5;6} \right)\)
Để ABCD.A’B’C’D’ là hình hộp thì A’B’C’D’ là hình bình hành.
Do đó, \(\overrightarrow {A’D’} = \overrightarrow {B’C’} \Rightarrow \left\{ \begin{array}{l}x – 5 = 4\\y = – 5\\z – 1 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 9\\y = – 5\\z = 5\end{array} \right.\). Suy ra \(D’\left( {9; – 5;5} \right)\)