Trả lời Câu hỏi Luyện tập 4 trang 10 SGK Toán 12 Kết nối tri thức – Bài 1. Tính đơn điệu và cực trị của hàm số. Hướng dẫn: Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại.
Câu hỏi/Đề bài:
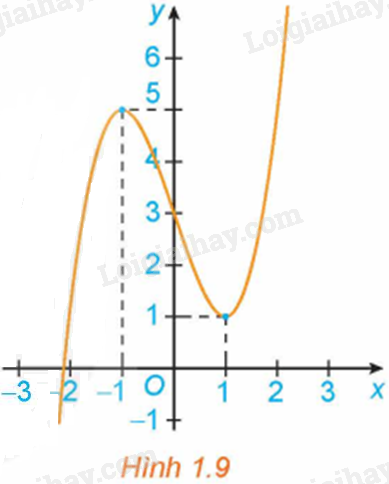
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.
Hướng dẫn:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( – \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} – h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} – h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải:
Từ đồ thị hàm số, ta có:
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 1\).
Hàm số đạt cực đại tại \(x = – 1\) và \({y_{C{\rm{D}}}} = y( – 1) = 5\)