Giải chi tiết Câu hỏi Hoạt động 3 trang 7 SGK Toán 12 Kết nối tri thức – Bài 1. Tính đơn điệu và cực trị của hàm số. Tham khảo: Cho hàm số \(y = f\left( x \right) = {x^3} – 3{x^2} + 2x + 1\).
Câu hỏi/Đề bài:
Cho hàm số \(y = f\left( x \right) = {x^3} – 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f’\left( x \right)\) và tìm các điểm x mà \(f’\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Hướng dẫn:
Cho hàm số \(y = f\left( x \right) = {x^3} – 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f’\left( x \right)\) và tìm các điểm x mà \(f’\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a) \(f’\left( x \right) = \left( {{x^3} – 3{x^2} + 2x + 1} \right)’ = 3{x^2} – 6x + 2\)
\(f’\left( x \right) = 0 \Leftrightarrow 3{x^2} – 6x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3 – \sqrt 3 }}{3}\\x = \frac{{3 + \sqrt 3 }}{3}\end{array} \right.\)
Vậy \(x = \frac{{3 – \sqrt 3 }}{3},x = \frac{{3 + \sqrt 3 }}{3}\) thì \(f’\left( x \right) = 0\)
b) Bảng biến thiên:
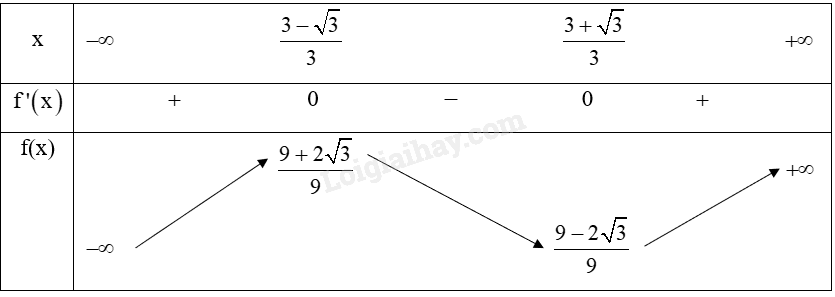
c) Hàm số \(y = f\left( x \right) = {x^3} – 3{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { – \infty ;\frac{{3 – \sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{3 + \sqrt 3 }}{3}; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {x^3} – 3{x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( {\frac{{3 – \sqrt 3 }}{3};\frac{{3 + \sqrt 3 }}{3}} \right)\).