Giải chi tiết Câu hỏi Hoạt động 3 trang 62 SGK Toán 12 Kết nối tri thức – Bài 7. Hệ trục tọa độ trong không gian. Gợi ý: Sử dụng kiến thức về tọa độ của điểm trong không gian để giải thích: Trong không gian Oxyz.
Câu hỏi/Đề bài:
Trong không gian Oxyz, cho vectơ \(\overrightarrow a \) tùy ý (H.2.41). Lấy điểm M sao cho \(\overrightarrow {OM} = \overrightarrow a \) và giải thích vì sao có bộ ba số (x; y; z) sao cho \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \).
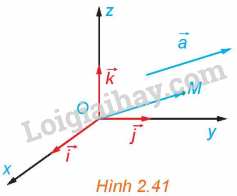
Hướng dẫn:
Sử dụng kiến thức về tọa độ của điểm trong không gian để giải thích: Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x; y; z) duy nhất sao cho \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết \(M = \left( {x;y;z} \right)\) hoặc \(M\left( {x;y;z} \right)\), trong đó x là hoành độ, y là tung độ, z là cao độ của M.
Lời giải:
Theo khái niệm tọa độ trong không gian ta có: \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \). Mà \(\overrightarrow {OM} = \overrightarrow a \) nên \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \). Do đó, có bộ ba số (x; y; z) sao cho \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \).