Sử dụng kiến thức về quy tắc hình hộp để tìm câu đúng: Cho hình hộp ABCD. A’B’C’D’. Khi đó, ta có. Giải và trình bày phương pháp giải Giải bài tập 2.27 trang 73 SGK Toán 12 tập 1 – Kết nối tri thức – Bài tập cuối Chương 2. Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào dưới đây là sai? A….
Đề bài/câu hỏi:
Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào dưới đây là sai?A. \(\overrightarrow {AB} + \overrightarrow {CC’} = \overrightarrow {AB’} \).B. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} \).C. \(\overrightarrow {AD} + \overrightarrow {BB’} = \overrightarrow {AD’} \).D. \(\overrightarrow {AB} + \overrightarrow {CC’} = \overrightarrow {AC’} \).
Hướng dẫn:
Sử dụng kiến thức về quy tắc hình hộp để tìm câu đúng: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} \)
Sử dụng kiến thức về hai vectơ bằng nhau để tìm câu đúng: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
Lời giải:
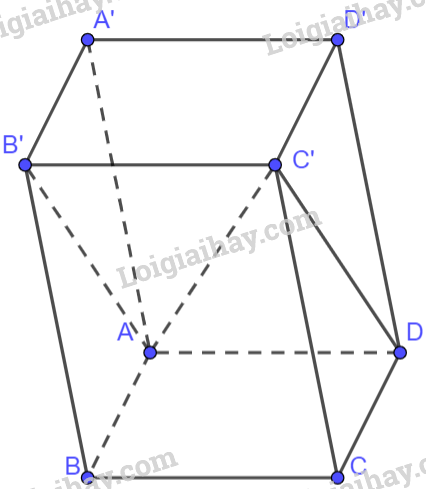
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \).
Vì DC’B’A là hình bình hành nên \(\overrightarrow {DC’} = \overrightarrow {AB’} \)
Do đó, \(\overrightarrow {AB} + \overrightarrow {CC’} = \overrightarrow {DC} + \overrightarrow {CC’} = \overrightarrow {DC’} = \overrightarrow {AB’} \) nên A đúng, D sai.
Vì ABCD.A’B’C’D’ là hình hộp nên \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} \) (quy tắc hình hộp) nên B đúng.
Ta có: \(\overrightarrow {AD} + \overrightarrow {BB’} = \overrightarrow {AD} + \overrightarrow {DD’} = \overrightarrow {AD’} \), do đó C đúng
Chọn D