Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ vectơ: Trong không gian Oxyz. Trả lời Giải bài tập 2.18 trang 65 SGK Toán 12 tập 1 – Kết nối tri thức – Bài 7. Hệ trục tọa độ trong không gian. Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có \(A\left( {1;1; – 1} \right),B\left( {0;3;0} \right),C’\left( {2; – 3;6} \right)\)….
Đề bài/câu hỏi:
Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có \(A\left( {1;1; – 1} \right),B\left( {0;3;0} \right),C’\left( {2; – 3;6} \right)\).a) Xác định tọa độ của điểm C.b) Xác định các tọa độ đỉnh còn lại của hình hộp.
Hướng dẫn:
Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ vectơ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).
Khi đó, \(\overrightarrow {MN} = \left( {{x_N} – {x_M};{y_N} – {y_M};{z_N} – {z_M}} \right)\).
Lời giải:
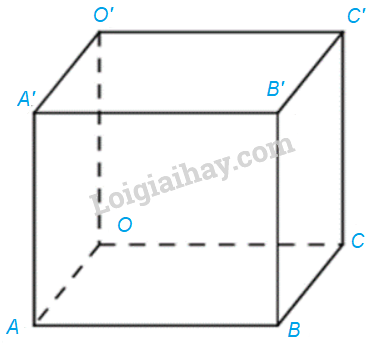
a) Ta có: O(0; 0; 0)
Vì OABC.O’A’B’C’ là hình hộp nên AOBC là hình bình hành. Do đó:\(\overrightarrow {OA} = \overrightarrow {CB} \Rightarrow \left\{ \begin{array}{l}{x_A} = {x_B} – {x_C}\\{y_A} = {y_B} – {y_C}\\{z_A} = {z_B} – {z_C}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_C} = {x_A} – {x_B} = 1\\{y_C} = {y_A} – {y_B} = – 2\\{z_C} = {z_A} – {z_B} = – 1\end{array} \right. \Rightarrow C\left( {1; – 2; – 1} \right)\)
b) Vì OABC.O’A’B’C’ là hình hộp nên
\(\overrightarrow {OO’} = \overrightarrow {CC’} \Rightarrow \left\{ \begin{array}{l}{x_{O’}} = {x_{C’}} – {x_C} = 1\\{y_{O’}} = {y_{C’}} – {y_C} = – 1\\{z_{O’}} = {z_{C’}} – {z_C} = 7\end{array} \right. \Rightarrow O’\left( {1; – 1;7} \right)\)
\(\overrightarrow {AA’} = \overrightarrow {CC’} \Rightarrow \left\{ \begin{array}{l}{x_{A’}} – {x_A} = {x_{C’}} – {x_C} = 1\\{y_{A’}} – {y_A} = {y_{C’}} – {y_C} = – 1\\{z_{A’}} – {z_A} = {z_{C’}} – {z_C} = 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{A’}} = 2\\{y_{A’}} = 0\\{z_{A’}} = 6\end{array} \right. \Rightarrow A’\left( {2;0;6} \right)\)
\(\overrightarrow {BB’} = \overrightarrow {CC’} \Rightarrow \left\{ \begin{array}{l}{x_{B’}} – {x_B} = \left( {{x_{C’}} – {x_C}} \right) = 1\\{y_{B’}} – {y_B} = \left( {{y_{C’}} – {y_C}} \right) = – 1\\{z_{B’}} – {z_B} = \left( {{z_{C’}} – {z_C}} \right) = 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{B’}} = 1\\{y_{B’}} = 2\\{z_{B’}} = 7\end{array} \right. \Rightarrow B’\left( {1;2;7} \right)\)