Bài tập 1.46 trang 44 Toán 12 tập 1 – Kết nối tri thức: Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4km

Đề bài/câu hỏi:

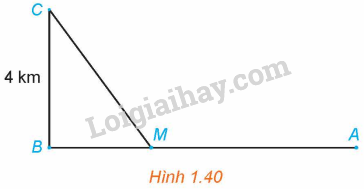
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10km. Tổng chi phí lắp đặt cho 1km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Xác định vị trí điểm M trên đoạn AB (điểm nối dây từ đất liền ra đảo) để tổng chi phí lắp đặt là nhỏ nhất.

Hướng dẫn:

Sử dụng kiến thức về cách giải bài toán tối ưu hóa đơn giản để tính:

Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.

Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số \(Q = Q\left( x \right)\).

Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số \(Q = Q\left( x \right)\) bằng các phương pháp đã biết và kết luận.

Lời giải:

Đặt \(MB = x\left( {km,0 \le x \le 10} \right)\), khi đó, \(AM = 10 – x\) (km) và \(MC = \sqrt {M{B^2} + C{B^2}} = \sqrt {{x^2} + 16} \) (km)

Khi đó, chi phí nối điện từ A đến C là: \(f\left( x \right) = 30\left( {10 – x} \right) + 50\sqrt {{x^2} + 16} \) (triệu đồng)

Ta có: \(f’\left( x \right) = – 30 + \frac{{50x}}{{\sqrt {{x^2} + 16} }} = 0 \Leftrightarrow \frac{x}{{\sqrt {{x^2} + 16} }} = \frac{3}{5} \Leftrightarrow 25{x^2} = 9{x^2} + 144 \Leftrightarrow x = 3\) (do \(0 \le x \le 10\))

Ta có: \(f\left( 0 \right) = 500;f\left( 3 \right) = 460,f\left( {10} \right) = 100\sqrt {29} \) nên chi phí nhỏ nhất là 460 triệu đồng khi \(x = 3\)

Vậy M cách B một khoảng 3km trên đoạn AB (điểm nối dây từ đất liền ra đảo) thì tổng chi phí lắp đặt là nhỏ nhất.