Lời giải Câu hỏi Vận dụng 5 trang 40 SGK Toán 12 Chân trời sáng tạo – Giải mục 4 trang 38 – 39 – 40 SGK Toán 12 tập 2. Gợi ý: Do \(\left( P \right) \bot \left( {Oxy} \right)\), mà vectơ pháp tuyến \(\vec n\) của \(\left( {Oxy} \right)\.
Câu hỏi/Đề bài:
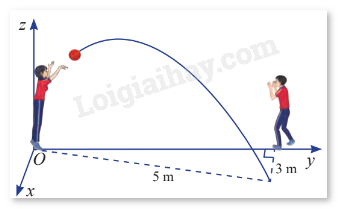
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam 3 m, cách bạn nữ 5 m. Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( P \right)\) vuông góc với mặt đất. Hãy viết phương trình của \(\left( P \right)\) trong không gian \(Oxyz\) được mô tả trong hình vẽ.
Hướng dẫn:
Do \(\left( P \right) \bot \left( {Oxy} \right)\), mà vectơ pháp tuyến \(\vec n\) của \(\left( {Oxy} \right)\) có giá vuông góc với \(\left( {Oxy} \right)\), nên giá của \(\vec n\) song song hoặc nằm trên \(\left( P \right)\). Như vậy \(\vec n\) là một vectơ chỉ phương của \(\left( P \right)\).
Mặt khác, theo hình vẽ, gọi \(A\) là điểm rơi của quả bóng trên mặt đất. Dễ dàng thấy được \({z_A} = 0\) và \({x_A} = 3\). Trên mặt phẳng \(\left( {Oxy} \right)\), sử dụng định lý Pythagore để xác định \({y_A}\) . Mặt phẳng \(\left( P \right)\) đi qua \(O\) và \(A\) nên \(\overrightarrow {OA} \) là một vectơ chỉ phương khác của \(\left( P \right)\). Dễ thấy rằng \(\overrightarrow {OA} \) và \(\vec n\) không cùng phương, từ đó tính tích có hướng của hai vectơ \(\overrightarrow {OA} \) và \(\vec n\) để tìm được một vectơ pháp tuyến của \(\left( P \right)\).
Lời giải:
Mặt phẳng \(\left( {Oxy} \right)\) có một vectơ pháp tuyến là \(\vec n = \left( {0;0;1} \right)\).
Do \(\left( P \right) \bot \left( {Oxy} \right)\), mà vectơ pháp tuyến \(\vec n\) của \(\left( {Oxy} \right)\) có giá vuông góc với \(\left( {Oxy} \right)\), nên giá của \(\vec n\) song song hoặc nằm trên \(\left( P \right)\). Như vậy \(\vec n\) là một vectơ chỉ phương của \(\left( P \right)\).
Mặt khác, theo hình vẽ, gọi \(A\) là điểm rơi của quả bóng trên mặt đất. Dễ dàng thấy được \({z_A} = 0\) và \({x_A} = 3\). Trên mặt phẳng \(\left( {Oxy} \right)\), ta có \(OA = 5\) và \({y_A} > 0\). Như vậy tung độ của \(A\) là \({y_A} = \sqrt {{5^2} – {3^2}} = 4\). Vậy ta có \(A\left( {3;4;0} \right)\)
Theo hình vẽ,\(\left( P \right)\) đi qua điểm \(O\left( {0;0;0} \right)\) và \(A\left( {3;4;0} \right)\), nên \(\overrightarrow {OA} \left( {3;4;0} \right)\) là một vectơ chỉ phương khác của \(\left( P \right)\). Ta dễ thấy rằng \(\vec n = \left( {0;0;1} \right)\) và \(\overrightarrow {OA} \left( {3;4;0} \right)\) là hai vectơ không cùng phương, do đó \(\vec n\) và \(\overrightarrow {OA} \) là một cặp vectơ chỉ phương của \(\left( P \right)\).
Như vậy một vectơ pháp tuyến của \(\left( P \right)\) là:
\(\overrightarrow {{n_{\left( P \right)}}} = \left[ {\vec n,\overrightarrow {OA} } \right] = \left( {0.0 – 1.4;1.3 – 0.0;0.4 – 0.3} \right) = \left( { – 4;3;0} \right)\).
Vậy phương trình mặt phẳng \(\left( P \right)\) đi qua \(O\left( {0;0;0} \right)\) và có một vectơ pháp tuyến \(\overrightarrow {{n_{\left( P \right)}}} = \left( { – 4;3;0} \right)\) là \( – 4\left( {x – 0} \right) + 3\left( {y – 0} \right) + 0\left( {z – 0} \right) = 0 \Leftrightarrow – 4x + 3y = 0\)