Lời giải Câu hỏi Thực hành 2 trang 9 SGK Toán 12 Chân trời sáng tạo – Bài 1. Tính đơn điệu và cực trị của hàm số. Hướng dẫn: Xác định tập xác định D, đạo hàm f’(x) và lập bảng biến thiên.
Câu hỏi/Đề bài:
Xét tính đơn điệu của các hàm số sau:
a) \(f(x) = {x^3} – 6{x^2} + 9x\)
b) \(g(x) = \frac{1}{x}\)
Hướng dẫn:
Xác định tập xác định D, đạo hàm f’(x) và lập bảng biến thiên
Lời giải:
a) \(f(x) = {x^3} – 6{x^2} + 9x\)
Tập xác định: \(D = \mathbb{R}\)
\(f'(x) = 3{x^2} – 12x + 9\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Bảng biến thiên:
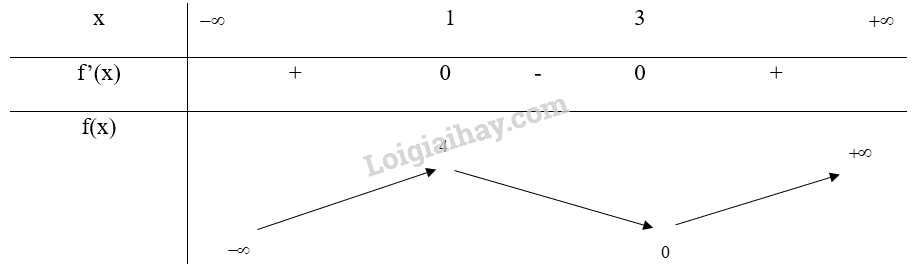
Vậy hàm số \(f(x) = {x^3} – 6{x^2} + 9x\) đồng biến trên các khoảng (\( – \infty \); 1) và (0; \( + \infty \)), nghịch biến trên khoảng (1; 3)
b) \(g(x) = \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
\(g'(x) = – \frac{1}{{{x^2}}}\)
Vì \({x^2} > 0\forall x \in \mathbb{R}\backslash \{ 0\} \) nên \(g'(x) < 0\forall x \in \mathbb{R}\backslash \{ 0\} \)
Bảng biến thiên:
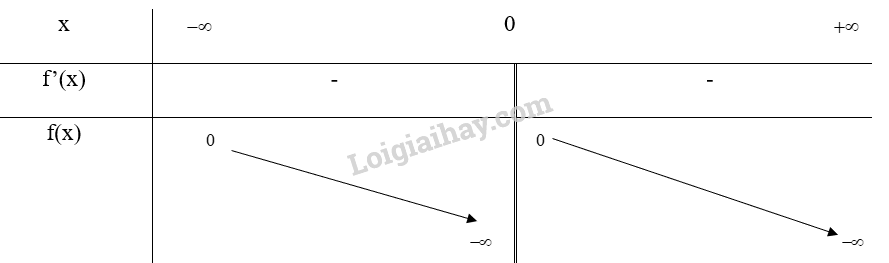
Vậy hàm số \(g(x) = \frac{1}{x}\) nghịch biến trên các khoảng (\( – \infty \); 0) và (0; \( + \infty \))