Đáp án Câu hỏi Thực hành 1 trang 13 SGK Toán 12 Chân trời sáng tạo – Bài 2. Tích phân. Gợi ý: Tìm một nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right)\).
Câu hỏi/Đề bài:
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {e^x}\), trục hoành, trục tung và đường thẳng \(x = 1\).
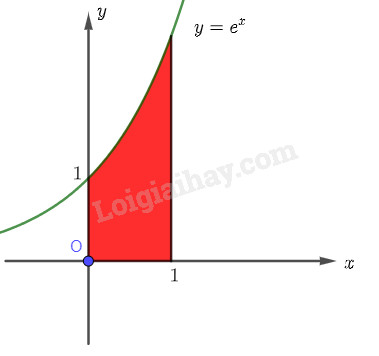
Hướng dẫn:
Tìm một nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right)\), sau đó sử dụng công thức để tính diện tích hình thang cong \(S = F\left( b \right) – F\left( a \right)\).
Lời giải:
Ta có hàm số \(y = f\left( x \right) = {e^x}\) liên tục và dương trên đoạn \(\left[ {0;1} \right]\).
Ta có \(\int {f\left( x \right)dx} = \int {{e^x}dx} = {e^x} + C\), từ đó suy ra \(F\left( x \right) = {e^x}\) là một nguyên hàm của \(f\left( x \right) = {e^x}\).
Diện tích hình thang cong cần tính là: \(S = F\left( 1 \right) – F\left( 0 \right) = {e^1} – {e^0} = e – 1\).