Giải Câu hỏi Khám phá trang 75 SGK Toán 12 Chân trời sáng tạo – Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm. Tham khảo: Khi biểu diễn mẫu số liệu liên tục bởi biểu đồ tần số có dạng cột.
Câu hỏi/Đề bài:
a) Trong biểu đồ ở Khởi động, cột thứ nhất biểu diễn số lượng học sinh có chiều cao từ 160cm đến dưới 164cm; cột thứ hai biểu diễn số lượng học sinh có chiều cao từ 164cm đến dưới 168cm, … .
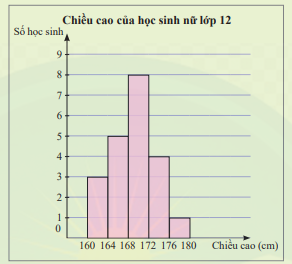
Hãy lập bảng tần số ghép nhóm cho mẫu số liệu ở , xác định giá trị đại diện của mỗi nhóm và tính số trung bình của mẫu số liệu ghép nhóm.
b) Xét mẫu số liệu mới gồm các giá trị đại diện của các nhóm, tần số của mỗi giá trị đại diện bằng tần số của nhóm tương ứng. Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu mới.
Hướng dẫn:
a) Khi biểu diễn mẫu số liệu liên tục bởi biểu đồ tần số có dạng cột, các cột thường được vẽ kề nhau. Ta quy ước: cột có đầu mút trái là a và có đầu mút phải là b trên trục hoành biểu diễn cho tần số của nhóm [a; b). Giá trị đại diện của nhóm [a; b) là \(c = \frac{1}{2}(a + b)\)
b) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} – \overline x )^2} + {n_2}{({c_2} – \overline x )^2} + … + {n_k}{({c_k} – \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + … + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + … + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Lời giải:
a) 
b) 
Cỡ mẫu: n = 21
Giá trị trung bình của mẫu số liệu mới: \(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + … + {n_k}{c_k}) = \frac{1}{{21}}(3.162 + 5.166 + 8.170 + 4.174 + 1.178) = \frac{{3550}}{{21}}\)
Phương sai của mẫu số liệu mới: \({S^2} = \frac{1}{n}[{n_1}{({c_1} – \overline x )^2} + {n_2}{({c_2} – \overline x )^2} + … + {n_k}{({c_k} – \overline x )^2}] = \frac{1}{{21}}[3{(162 – \frac{{3550}}{{21}})^2} + 5{(166 – \frac{{3550}}{{21}})^2} + … + 1{(178 – \frac{{3550}}{{21}})^2}] = \frac{{8000}}{{441}}\)
Độ lệch chuẩn của mẫu số liệu mới: \(\sigma = \sqrt {{S^2}} = \sqrt {\frac{{8000}}{{441}}} = \frac{{40\sqrt 5 }}{{21}}\)