Giải Câu hỏi Khám phá 2 trang 21 SGK Toán 12 Chân trời sáng tạo – Bài 3. Đường tiệm cận của đồ thị hàm số. Hướng dẫn: Quan sát đồ thị.
Câu hỏi/Đề bài:
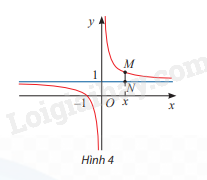
Cho hàm số \(y = \frac{{x + 1}}{x}\) có đồ thị như Hình 4.
a) Tìm \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x},\mathop {\lim }\limits_{x \to – \infty } = \frac{{x + 1}}{x}\)
b) Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to – \infty \)
Hướng dẫn:
Quan sát đồ thị
Lời giải:
a) Từ đồ thị ta thấy:
Khi \(x \to + \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x} = 1\)
Khi \(x \to – \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to – \infty } = \frac{{x + 1}}{x} = 1\)
b) MN = y – 1 = \(\frac{{x + 1}}{x} – 1 = \frac{1}{x}\)
Khi \(x \to + \infty \) hoặc \(x \to – \infty \) thì MN tiến dần về 0