Áp dụng công thức tính công \(A = Fs\cos \alpha \. Phân tích, đưa ra lời giải Giải bài tập 8 trang 51 SGK Toán 12 tập 1 – Chân trời sáng tạo – Bài 1. Vectơ và các phép toán trong không gian. Một lực tĩnh điện \(\overrightarrow F \) tác động lên điện tích điểm M trong điện trường đều làm cho…
Đề bài/câu hỏi:
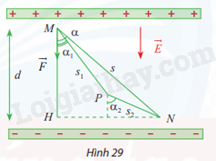
Một lực tĩnh điện \(\overrightarrow F \) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình 29). Biết \(q = {2.10^{ – 12}}C\), vectơ điện trường có độ lớn \(E = 1,{8.10^5}\)N/C và d = MH = 5mm. Tính công A sinh bởi lực tĩnh điện \(\overrightarrow F \).
Hướng dẫn:
Áp dụng công thức tính công \(A = Fs\cos \alpha \)
Lời giải:
Đổi: 5mm = 0,005m
Gọi K là điểm thuộc MH sao cho \(PK \bot MH\), L là điểm thuộc HN sao cho \(PL \bot HN\)
\({A_{MNP}} = {A_{MP}} + {A_{PN}} = {F_d}.MP\cos {\alpha _1} + {F_d}.PN\cos {\alpha _2}\)
\( \Leftrightarrow {A_{MNP}} = qE.\frac{{MK}}{{\cos {\alpha _1}}}.\cos {\alpha _1} + qE.\frac{{PL}}{{\cos {\alpha _2}}}.\cos {\alpha _2}\)
\( \Leftrightarrow {A_{MNP}} = qE(MK + PL) = qE(MK + KH) = qE.MH = {2.10^{ – 12}}.1,{8.10^5}.0,005 = 1,{8.10^{ – 9}}J\)