Chọn trục \(Ox\) sao cho \(O\) trùng với đỉnh của khối chóp. Dựng một mặt phẳng cắt trục \(Ox\) tại điểm có hoành độ \(x\). Phân tích và giải Giải bài tập 8 trang 27 SGK Toán 12 tập 2 – Chân trời sáng tạo – Bài 3. Ứng dụng hình học của tích phân. Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng (a) và chiều…
Đề bài/câu hỏi:
Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng \(a\) và chiều cao bằng \(h\).
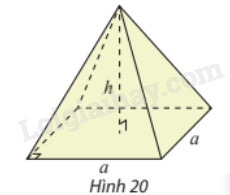
Hướng dẫn:
Chọn trục \(Ox\) sao cho \(O\) trùng với đỉnh của khối chóp.
Dựng một mặt phẳng cắt trục \(Ox\) tại điểm có hoành độ \(x\). Mặt phẳng đó cắt khối chóp \(O.ABCD\) với mặt cắt là hình vuông \(A’B’C’D’\).
Tính độ dài cạnh \(A’B’\), sau đó tính diện tích mặt cắt \(S\left( x \right) = {S_{A’B’C’D’}}\), từ đó tính thể tích khối chóp tứ giác đều \(O.ABCD\) theo công thức \(V = \int\limits_0^h {S\left( x \right)dx} \).
Lời giải:
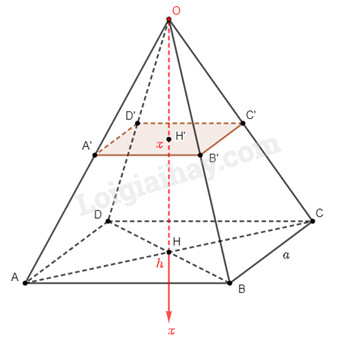
Xét khối chóp đều \(O.ABCD\) có chiều cao \(OH = h\), độ dài cạnh đáy \(AB = a\)
Chọn trục \(Ox\) sao cho \(O\) trùng với đỉnh của khối chóp, mặt đáy \(\left( {ABCD} \right)\) cắt trục \(Ox\) tại điểm có hoành độ \(\) như hình vẽ.
Dựng một mặt phẳng cắt trục \(Ox\) tại điểm có hoành độ \(x\). Mặt phẳng đó cắt khối chóp \(O.ABCD\) với mặt cắt là hình vuông \(A’B’C’D’\).
Ta có \(\frac{{B’C’}}{{BC}} = \frac{{OB’}}{{OB}} = \frac{{OH’}}{{OH}} = \frac{x}{h} \Rightarrow B’C’ = \frac{a}{h}x\).
Diện tích mặt cắt \(A’B’C’D’\) là \(S\left( x \right) = {\left( {\frac{a}{h}x} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\).
Vậy thể tích khối chóp đều \(O.ABCD\) là \(V = \int\limits_0^h {\left( {\frac{{{a^2}}}{{{h^2}}}{x^2}} \right)dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)